∠АВС = 80°.
Объяснение:
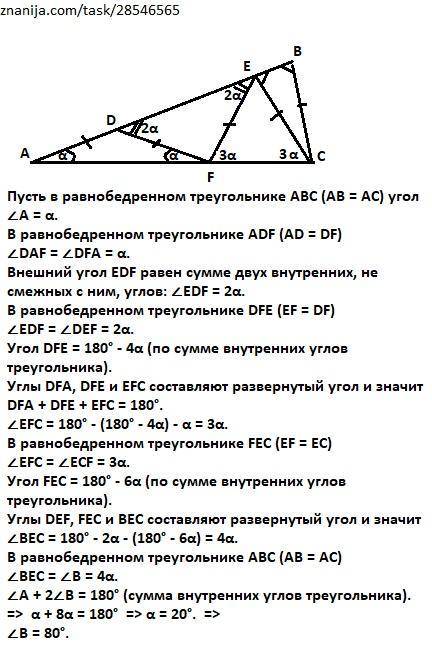
Пусть в равнобедренном треугольнике АВС (АВ = АС) угол
∠А = α.
В равнобедренном треугольнике ADF (AD = DF)
∠DAF = ∠DFA = α.
Внешний угол EDF равен сумме двух внутренних, не смежных с ним, углов: ∠EDF = 2α.
В равнобедренном треугольнике DFЕ (EF = DF)
∠EDF = ∠DEF = 2α.
Угол DFE = 180° - 4α (по сумме внутренних углов треугольника).
Углы DFA, DFE и EFС составляют развернутый угол и значит
DFA + DFE + EFС = 180°.
∠EFC = 180° - (180° - 4α) - α = 3α.
В равнобедренном треугольнике FЕС (EF = ЕС)
∠EFС = ∠EСF = 3α.
Угол FEС = 180° - 6α (по сумме внутренних углов треугольника).
Углы DЕF, FEC и BEC составляют развернутый угол и значит
∠ВЕС = 180° - 2α - (180° - 6α) = 4α.
В равнобедренном треугольнике АВС (АВ = АС)
∠ВЕС = ∠В = 4α.
∠А + 2∠В = 180° (сумма внутренних углов треугольника). => α + 8α = 180° => α = 20°. =>
∠В = 80°.
∠АВС = 80°.
Объяснение:
Пусть в равнобедренном треугольнике АВС (АВ = АС) угол
∠А = α.
В равнобедренном треугольнике ADF (AD = DF)
∠DAF = ∠DFA = α.
Внешний угол EDF равен сумме двух внутренних, не смежных с ним, углов: ∠EDF = 2α.
В равнобедренном треугольнике DFЕ (EF = DF)
∠EDF = ∠DEF = 2α.
Угол DFE = 180° - 4α (по сумме внутренних углов треугольника).
Углы DFA, DFE и EFС составляют развернутый угол и значит
DFA + DFE + EFС = 180°.
∠EFC = 180° - (180° - 4α) - α = 3α.
В равнобедренном треугольнике FЕС (EF = ЕС)
∠EFС = ∠EСF = 3α.
Угол FEС = 180° - 6α (по сумме внутренних углов треугольника).
Углы DЕF, FEC и BEC составляют развернутый угол и значит
∠ВЕС = 180° - 2α - (180° - 6α) = 4α.
В равнобедренном треугольнике АВС (АВ = АС)
∠ВЕС = ∠В = 4α.
∠А + 2∠В = 180° (сумма внутренних углов треугольника). => α + 8α = 180° => α = 20°. =>
∠В = 80°.

Найдем ее основания: (см. рисунок)
ОО1АВ - прямоугольная трапеция, О1Q=AB=h - ее высота. По теореме Пифагора
Поскольку треугольники TCO иTDO1 - подобны и соотношение сторон равно R:r=4, то
По теореме Пифагора
Тогда
Поскольку треугольники TCS иTDR также подобны и соотношение сторон равно, то CS=4*12=48.
Тогда ABCD - равнобедренная трапеция с высотой 48 cм и средней линией 48+12=60 см. Ее площадь будет равна
S=60*48=2880 см^2.