Объяснение:
АС - основание. Проводим высоты АН2, СН3 и ВН1 соответственно из углов А, С и В.
Высота ВН1, проведённая к основанию является медианой и биссектриссой угла В, тогда СН1 = 12/6 =2
Рассмотрим треугольник ВСН1: cos C = СН1 / ВС = 6/18 =1/3
Расмотрим треугольник АСН2: cos C = CH2 / AC, отсюда СН2 = АС*cos C = 12 * 1/3 = 4
Тогда ВН2 = 18-4 = 14
Согласно теореме: в любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному, т.е. треугольник ВН2Н3 подобен треугольнику АВС. к = ВН2/ВС = 14/18 = 7/9
Н3Н2 = 12*7/9 = 28/3 = 9
ответ;9
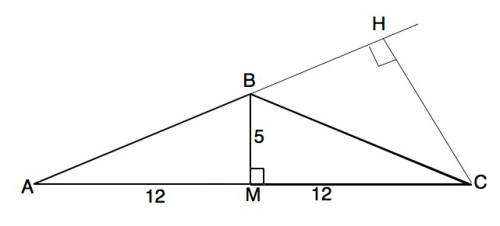
Медиана равнобедренного треугольника, проведенная к основанию, является и его высотой. АМ=МС=24^2=12 см, ВМ⊥АС. Из прямоугольного ∆ ВМС по т.Пифагора гипотенуза ВС=√(BM²+MC²)=13 см. Из прямоугольного ∆ ВМС синус угла при основании ВМ:ВС=5/13.
Проведем высоту СН к стороне АВ. Высота тупоугольного треугольника, проведенная из острого угла, проходит ВНЕ его и пересекает продолжение стороны. Треугольник АНС прямоугольный ( т.к.СН высота). АС - гипотенуза. Угол А=углу С ( ∆ АВС равнобедренный). Синус угла А=5/13. Искомая высота – катет СН=АС•sinA=24•5/13=9³/₁₃
BC = √[(7 - 2)² + (8 + 7)²] = √(25 + 225) = √250 = 5√10
AC = √[- 2 - 2)² + (5 + 7)²] = √(16 + 144) = √160 = 4√10
P = 3√10 + 5√10 + 4√10 = 12√10