Если на одной из двух прямых отложить несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
Пусть дан отрезок ВС.
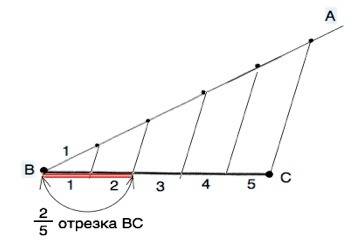
От конца В отрезка начертить луч и на нем от В отметить через равные промежутки 5 точек. Из пятой точки провести прямую через т.С отрезка ВС и провести параллельно ей прямые, пересекающие отрезок ВС. Этими прямыми ВС будет разделен на 5 равных частей. Любые две соседние части равны 2/5 исходного отрезка ВС.
m, n, k
найти: Sповерх.
Решение:
Пусть m=a, n=b, k=c, тогда:
Так как фигура - параллелепипед, следовательно, противоположные грани равны, и площади их равны.
площадь1=b*c
площадь2=a*c
площадь3=a*b
площадь поверхности= 2*площадь1 + 2*площадь2 + 2*площадь3= 2*bc+2*ac+2*ab=2*(bc+ac+ab)
ответ: 2*(bc+ac+ab)