Биссектрисы двух внешних углов и внутреннего угла треугольника пересекаются в центре вневписанной окружности.
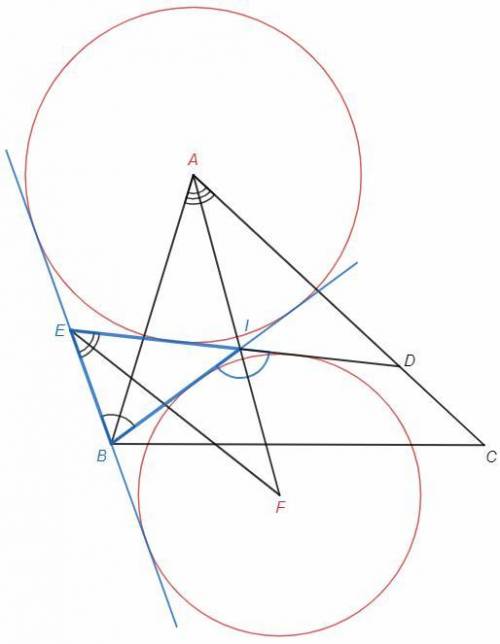
Центр вписанной окружности треугольника (I) является точкой пересечения биссектрис, AI - биссектриса ∠BAC
△BAI=△DAI (по двум сторонам и углу между ними)
∠BIF=∠DIF (смежные с равными)
AF - биссектриса внешнего угла ∠BID треугольника BEI
EF - биссектриса внутреннего угла ∠BEI
F - центр вневписанной окружности △BEI
BA - биссектриса внутреннего угла ∠EBI треугольника BEI
A - центр вневписанной окружности △BEI
Р=2(а+в)
а-одна сторона =х
в-вторая сторона=х-8
2(х+х-8)=36
4х-16=36
4х=52
х=13 см-одна сторона и противоположная ей
х-8=13-8=5 см -вторая сторона и противоположная ей
ответ: 5см,5см,13см,13см