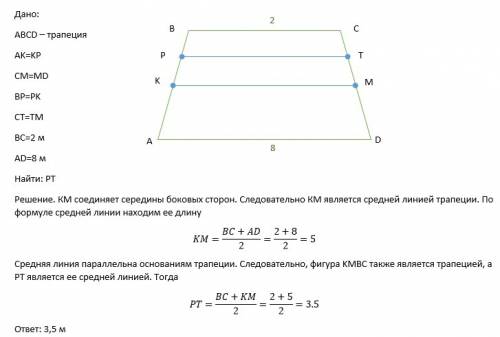
в условии ошибка, нужно так:
m не делится на n и имеет от деления на n тот же остаток
решение:
a,b - натуральные числа (целые части от деления)
r -остаток от деления
m=na+r
m+n=(m-n)b+r
m+n-r=(m-n)b
n+m-r делится на n и m-nесли m< =2n, тоn< n+m-r< 3n, следовательно оно равно 2nтогда m-n=r и при делении на него не может быть остатка r.значит m> 2nтогда n+m-r< 3(m-n), т.к. 4n< 2mзначит n+m-r=2(m-n), т.к. m-n на n по условию не делится.отсюда m=3n-r, m+n-r=4n-2r делится на n, отсюда r=n/2.значит m=5k, n=2k
m: n=5: 2
1) нет 2) да 3) нет 4) нет
Объяснение:
1) Если диагонали четырёхугольника взаимно перпендикулярны, то он может быть либо ромбом, либо квадратом. То есть не обязательно ромбом.
ответ: данное утверждение нельзя считать правильным.
2) У ромба все стороны равны между собой. Значит, его периметр всегда в 4 раза больше длины его стороны. А отношение 4 к 1 всегда равно 4.
ответ: это правильное утверждение.
3) Диагонали равны и у прямоугольника и у квадрата. Оба они четырёхугольники. Поэтому если диагонали у четырёхугольника равны, то он не обязательно должен быть прямоугольником, он может быть и квадратом.
ответ: данное утверждение нельзя считать правильным.
4) Это неправильно. Например, возьмём прямоугольник 5 х 10. Его периметр = 30 см, отношение 30 : 10 = 3. А в прямоугольнике 5 х 20 периметр равен 50, а отношение 50 : 20 = 2,5, а не 3, как было в первом расчете.
ответ: данное утверждение нельзя считать правильным.