№1:  . №2:
. №2: 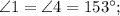
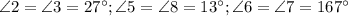 .
.
№1.
Пусть  , тогда
, тогда  - секущая.
- секущая.
Теорема: "При пересечении двух параллельных прямых секущей, сумма односторонних углов равна  .
.
 , по условию.
, по условию.
 и
и  - односторонние углы
- односторонние углы 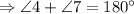
№2.
Обозначим данные прямые буквами 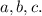
Пусть  - секущая прямых
- секущая прямых  и
и 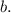
Теорема: "При пересечении двух параллельных прямых секущей, накрест лежащие углы равны".
 и
и 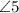 - накрест лежащие при пересечении
- накрест лежащие при пересечении  и
и  секущей
секущей  , однако
, однако 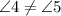 .
.

 и
и  - не параллельны.
- не параллельны.
============================================================
Свойство: "Вертикальные углы равны".
Свойство: "Сумма смежных углов равна  ".
".
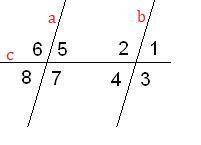
Рассмотрим углы, образовавшиеся при пересечении прямых  и
и 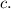
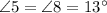 , по свойству вертикальных углов.
, по свойству вертикальных углов.
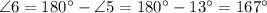 , по свойству смежных углов.
, по свойству смежных углов.
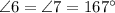 , по свойству вертикальных углов.
, по свойству вертикальных углов.
===========================================================
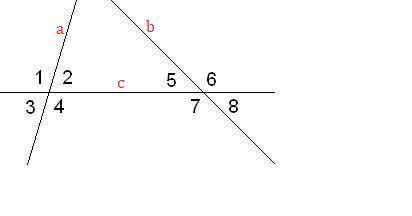
Рассмотрим углы, образовавшиеся при пересечении прямых  и
и  .
.
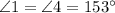 , по свойству вертикальных углов.
, по свойству вертикальных углов.
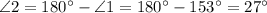 , по свойству смежных углов.
, по свойству смежных углов.
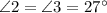 , по свойству вертикальных углов.
, по свойству вертикальных углов.
Строим сечение. Соединяем точку В с точкой К (серединой SC)
Проводим КМ || AB, Соединяем точку М с точкой А
Сечение ВКМА- трапеция.
КМ- средняя линия треугольника SCD и КМ=1/2 CD=1/2
В треугольнике BSC SK- медиана, но так как треугольник равносторонний, то и высота. По теореме Пифагора BK²=BC²-KC²=1-(1/2)²=3/4.
BK=√3/2.
Находим площадь равнобедренной трапеции : МК=1/2, АВ=1, ВК=МА=√3/2 ( см рисунок 2)
Проводим высоты КН и МР. ВН=РА=1/4
По теореме Пифагора
КН²=ВК²-ВН²=(√3/2)²-(1/4)²=3/4-1/16=12/16-1/16=11/16
КН=√11/4
S(сечения)=(АВ+КМ)КН/2=1/2 ·(1+1/2)√11/4=3√11/16
Объяснение: