Стальная болванка имеет форму правильной четырехугольной призмы со сторонами основания 0.4 м и высотой 1м, Сколько метров проволоки диаметром 5 мм можно изготовить из этой болванки?
ответ: 25600/π м или иначе 8148,7 м
Объяснение:
d=5мм=0,005 м => r сечения проволоки d:2=0.0025 м
——
Представим проволоку в виде цилиндра c радиусом основания 0, 0025 м и высотой - длиной проволоки – L. =>
L=V:S, где V- объем такого цилиндра, S - площадь основания ( сечения проволоки). Ѕ(осн)=πr²=π•0.0025²=0.00000625•π мм²
Так как проволоку нужно изготовить из всего металла, ее объем будет равен объему данной болванки.
Формула объема прямоугольной призмы V(б)=S•h.
Основанием Ѕ правильной четырехугольной призмы является квадрат.
V(пр)=0,4²•1=0.16 м²
L=0,16:0.00000625•π=25600/π или иначе 8148,7 м
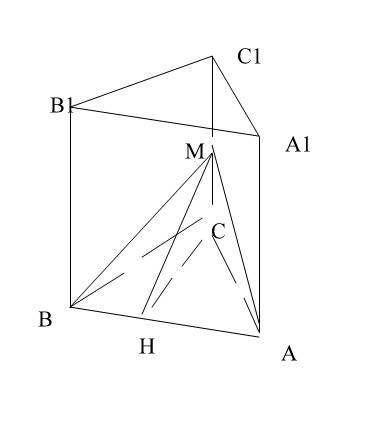
Дана прямая треугольная призма АВСА1В1С1.
Угол МНС=60 гр. НС-высота треугольника АВС.
Рассмотрим треугольник АВС и ВНС.
Эти треугольники подобны, следовательно, ВН/ВС = СН/АС = ВС/АВ.
Берем первое и последнее соотношение пропорции и получаем, что ВН = ВС^2 / АВ.
Треугольник ВНС-прямоугольный, следовательно, BC^2 = BH^2 + CH^2.
СН = (ВС *АС) / АВ
СН = (6*8)/10=4,8.
Рассмотрим треугольник НСС1-прямоугольный. Угол МНС=60 гр, следовательно угол СС1Н=30 гр. Катет, лежащий, напротив угла 30 градусов, равен половине гипотенузы.
СН = 1/2 МН
МН = 2*4,8=9,6.
Вроде так.
В треугольнике АСД угол А=90-58=32, угол А = углу Д = 32 как углы при основании равнобедренного треугольника ( он равнобедреный по условию задачи) следовательно угол С=116
углы трапеции соответственно равны А=90, В=90, С=148 .Д=32