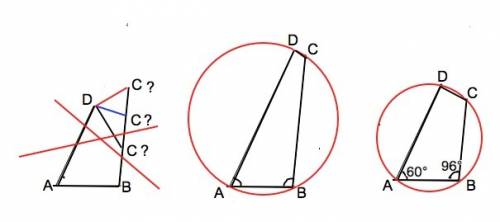
Задача имеет решение только если АВСD – четырехугольник, вписанный в окружность. (см. рисунки вложения)
В противном случае величину углов АDC и DCB вычислить невозможно, они могут принимать различное значения, лишь бы их сумма была равна разности между суммой углов четырехугольника и суммой углов АВС и BAD, т.е. 204°
-----------
Четырехугольник можно вписать в окружность, если сумма его противолежащих углов равна 180º.
Тогда ∠ADC=180°-∠ABC=180°-96=84°
∠BCD=180°-∠BAD=180°-60°=120°⇒
∠BCD-∠ADC=120°-84°=36°.
1. АОС = DOB
2. КМN=KPN
Объяснение:
1.Розглянемо трикутники АОС і DOB . В них СО = OB ( за умовою) . CD Х АВ в т. О. ( це пояснює те, що СД поділений на 2 рівні частини, тобто СО= ОД) Виходить, що ОА=ОВ.
Отже трикутник АОС і ДОВ є рівнобеденими ( за двома сторонами і спільною вершиною)
Доведено
2. Розглянемо трикутники КМН і КРН. В них МН = КР ( за умовою) , КМ = РН ( за умовою) , кут НКР = КНР=МНК=МКН ( за умовою) . К прямокутнику всі кути рівні =90°, тобто кут Р = куту М.
Виходить, що дані трикутники рівні за 2 сторонами, кутами при основі і вершиною цих трикутників.
Доведено
Значит, что этот внутренний угол - это угол вершины равнобедренного треугольника, так как он не может быть углом при основании (тогда бы их было два угла по 100, а это невозможно). Из этого следует, что два других угла равны (так как они при основании равнобедренного треугольника). Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним, сумма этих углов будет равна 80. (еще можно посчитать как сумма всех углов треугольника минус известный угол 180-100=80), а так как они равны, то делим на 2, значит 80/2=40.
ответ: углы в треугольнике 40, 40 и 100