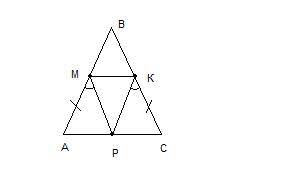
1)АВС - равнобедренный, тогда уголА=углуС(при основании), также
угол AMP=углу PKC и AM=KC(по условию),
то треугольникAMP=треугольникуPKC (по стороне и 2ум прилежащим углам), значит
все элементы в них равны, тогда АР=РС, значит ВР-медиана,
а в равнобедренном треугольнике медиана, проведенная из угла между боковыми сторонами является ещё и высотой и биссектрисой.
2)АМ=КС(по условию), причем уголА=углуС(при основании), значит
АМКС - равнобедренная трапеция, тогда МК параллельно АС.
т.к.ВР и медиана и биссектриса и высота [см. 1) доказательство],
то ВР перпендикулярно АС, но т.к. МК параллельно АС, то
ВР перпендикулярно МК
Надеюсь удачи ! )
Проведём две высоты трапеции ВМ и СN. Углы АВМ и ДСN равны по 30 градусов поскольку трапеция равнобедренная , а В=120. Против угла 30 градусов лежит катет вдвое меньший гипотенузы, значит АМ=3. АД=АМ+ МN+NВД=3+4+3=10. Высота Н=АВcos30=(6на корень из 3)/2. Площадь трапеции равна S=(4+10)/2 умноженное на (6 корней из 3)/2=36,37.