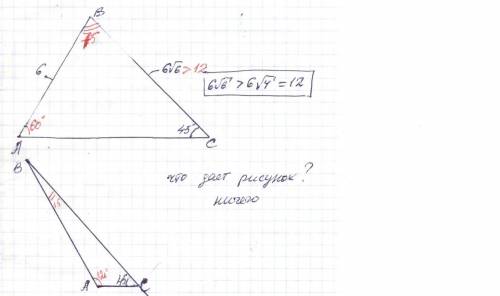
Найдите углы A и B треугольника ABC, если AB=12 см, BC=6√6 см, угол C= 45°.
ответ: 60° , 75° или 120° , 15° .
Объяснение:
По теореме синусов : BC / sin(∠A) =AB / sin(∠C ) ⇔
6√6/sin(∠A)=12/sin45°⇔sin(∠A) =6√6*sin45°/12=6√6 *(√2/2) / 12 = 3 /2 ⇒
∠A= 60° или ∠A= 120° . Оба верны ∠A > ∠C , т.к. BC > AB
( в треугольнике против большой стороны лежит большой угол )
* * * BC > AB : BC = 6√6 > 6√4 = 12 = AB * * *
∠B = 180° - (∠A+√C) → ∠B = 75° или ∠B = 15° см. лишнее приложение
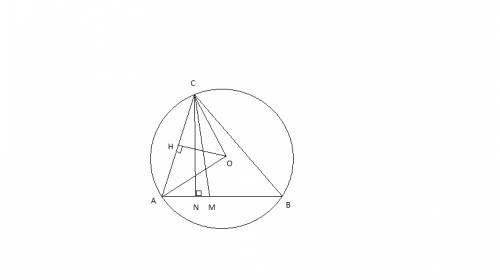
1-случай ( точка М находится правее точки N);
I. Построение:
Проведем r (радиусы) OC и ОА.
Проводим высоты ОН и СN.
II. Расчет:
1) Находим СN и ВN.
ΔОHС ≈ ΔBNC по 2-ум углам (∢СОН =∢СВА, т.к вписанный ∢СВА и центральный ∢СОА опираются на дугу АС, т.е. ∢СВА в 2 раза < ∢СОА, а ∢СОН = 1/2 ∢СОА, т.к. высота в равнобедренном треугольнике является и медианой и биссектрисой; ∢ОНС = ∢ВNС);
ΔOНC: ОС = 32,5; НС = 26; ОН = 19,5.
ΔВNС: СВ = 60; СN = ?; ВN = ?.
ОС/СВ = НС/СN = ОН/ВN; 32,5/60 = 26/СN = 19,5/ВN; СN = 48, ВN = 36.
2) Найдем NМ.
NМ = 14.
3) Найдем S ΔВМС.
S ΔCNB = 1/2 · 36 · 48 = 864.
S ΔCNM = 1/2 · 14 · 48 = 336.
S ΔCMB = 864 - 336 =528.
2-случай - по аналогии. Только точка М находится левее точки N.
Вложения