Диагональ прямоугольника делит его на два треугольника, отношение сторон которых равно отношению сторон "египетского треугольника". т.е. 3:4:5
Примем коэффициент отношения сторон за х.
Тогда при катетах 3х и 4х гипотенуза равна 5х.
Следовательно , диагональ здесь играет роль гипотенузы
5х=20
х=4
Один катет равен 3*4=12 см - это меньшая сторона прямоугольника
другой 4*4=16 см - это большая его сторона.
ответ: Большая сторона прямоугольника равна 16 см.
Задачу можно решить и через теорему Пифагора:
20²=(3х)²+(4х)²
400=9х²+16х²
25х²=400
х²=16
х=4 см
Но гораздо удобнее знать хотя бы несколько так называемых Пифагоровых троек, к которым относится и египетский треугольник.
S=a*b
Площадь прямоугольника равна произведению смежных сторон.
Док-во:
Дано: ABCD - прямоугольник;
а и b - стороны прямоугольника.\
Док-ать, что S=ab
Докозательство:
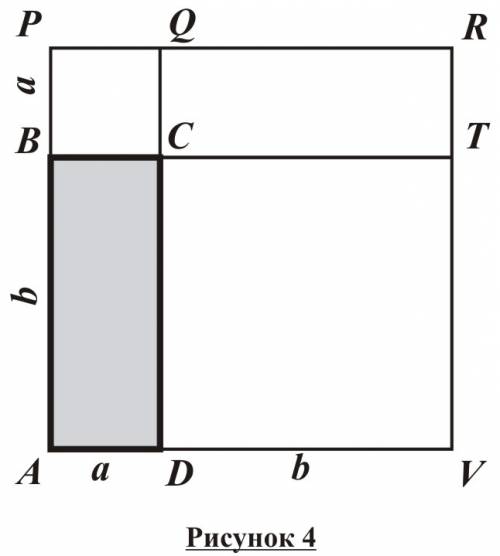
Достраиваем прямоугольник до квадрата сос тороной a+b
Т.к. площадь квадрата = квадрату его стороны,то площадь всего квадрата = (a+b)в квадрате.
С другой стороны,этот квадрат составлен из данного прямоугольника с площадью S,равного ему прямоугольника с площадью S (так как по свойству площадей,равные многоугольники имеют равные площади) и двух квадратов с площадями а^2 и b^2. Так как четырехугольник составлен из нескольких четырехугольников , то , по свойству площадей,его площадь равнв сумме площадей этих четырехугольников:
(а+b)^2=S+S+a^2+b^2 или a^2+2ab+b^2=2S+a^2+b^2
получаем: S=ab
Теорема доказана.