Диагонали ромба точкой пересечения делятся пополам (как и у параллелограмма)
Диагонали ромба взаимно перпендикулярны
Диагонали ромба являются биссектрисами его углов
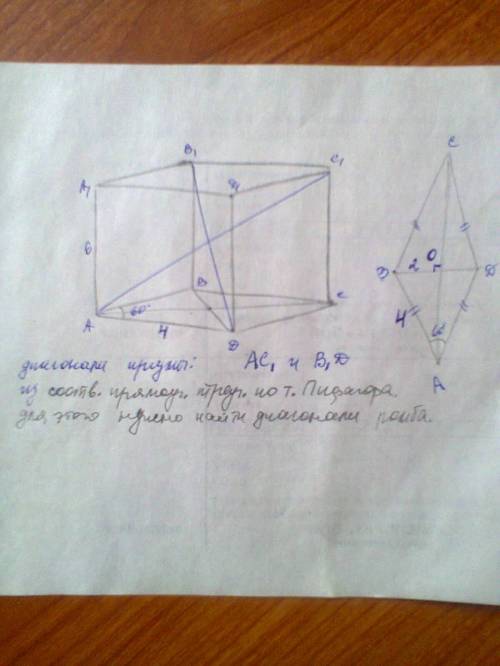
из треуг.BOA: угол BAO=30, катет BO = 4/2 = 2 (катет против угла в 30 град.=половине гипотенузы) и по т.Пифагора второй катет = корень(4^2-2^2) = 2корень(3)
следовательно, диагонали ромба равны
BD = 2BO = 4
AC = 2AO = 4корень(3)
AC1^2 = AC^2 + CC1^2 = 4*4*3 + 6*6 = 4*(12+9) = 4*21
AC1 = 2корень(21)
B1D^2 = BD^2 + CC1^2 = 4+36 = 40
B1D = 2корень(10)
Пусть данный ΔАВС, ∟A = 60 °, ∟B = 70 °, АВ = 2 см, AD = 1 см.
Найдем углы ΔBDC.
В ΔABD проведем медиану DK.
АК = КВ = 1 / 2АВ = 2: 2 = 1 см.
Рассмотрим ΔAKD - piвнобедрений (AD = АК = 1 см),
Если ∟A = 60 °, то ΔAKD - piвносторонний.
Итак, AD = АК = KD, ∟А = ∟AКD = ∟KDA = 60 °.
∟ВКD i ∟AKD - смежные, тогда ∟BKD + ∟AKD = 180 °.
∟BKD = 180 ° - 60 ° = 120 °.
ΔBKD - равнобедренный (KB = KD = 1 см), тогда
∟KBD = ∟KDB = (180 ° - 120 °): 2 = 30 °.
Рассмотрим ΔАВС:
∟A + ∟B + ∟C = 180 °. ∟C = 180 ° - (60 ° + 70 °); ∟C = 50 °.
∟B = ∟KBD + ∟DBC; ∟DBC = 70 ° - 30 ° = 40 °.
Рассмотрим ΔBDC:
∟DBC + ∟C + ∟BDC = 180 °.
40 ° + 50 ° + ∟BDC = 180 °. ∟BDC = 180 ° - 90 ° = 90 °.
Biдповидь: ∟BDC = 90 °; ∟DBC = 40 °; ∟C = 50 °
Объяснение: