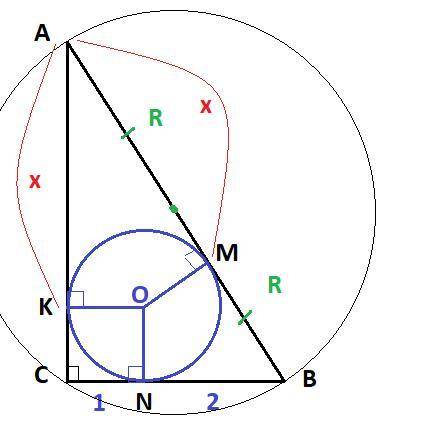
Дано : ΔABC, ∠C = 90°, CN = 1 см, NB = 2 см,
вписанная окружность (O; r)
Найти : S, r, R
Так как окружность вписана в треугольник, то стороны треугольника являются касательными к окружности. Радиус, проведённый в точку касания, перпендикулярен касательной в этой точке.
ON⊥CB, OK⊥AC, OM⊥AB
⇒ CKON - квадрат со стороной, равной радиусу вписанной окружности
⇒ r = CK = KO = JN = CN = 1 см
Отрезки касательных к окружности, проведённые из одной точки, равны
BM = BN = 2 см; AK = AM = x см
ΔABC :
BC = CN + BN = 1 см + 2 см = 3 см
AC = AK + KC = (x + 1) см
AB = AM + MB = (x + 2) см
Площадь прямоугольного треугольника можно вычислить через полупроизведение катетов или через произведение полупериметра на радиус вписанной окружности.
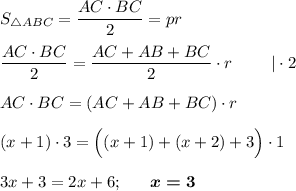
AC = x + 1 = 4 см; AB = x + 2 = 5 см
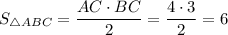 см²
см²
Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы
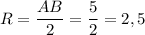 см
см
ответ : S = 6 см², r = 1 см, R = 2,5 см
Площадь по формуле Герона
Полупериметр
p = (13+14+15)/2 = 7
S² = 21*8*7*6 = 7056
S = √7056 = 81.
Делим площадь в отношении 1:2
s = 1/3*81 = 27 см² - площадь сечения - ОТВЕТ
2)
Объем пирамиды по формуле
V = 1/3*S*H
S - площадь сечения, H - высота.
Сторона квадрата в основании
a = D : √2 = = 3 см
Площадь сечения
S = а² = 3² = 9 см²
V = 1/3*9*12 = 36 см³ - объем пирамиды - ОТВЕТ
3)
V = 1/3*S*H = 1/3*6*10*15 = 300 см³ - ОТВЕТ