Центром описанной окружности треугольника является точка пересечения срединных перпендикуляров.
Для остроугольного треугольника этот центр будет в треугольнике.
Построение.
Построить нужный треугольник не составляет труда.
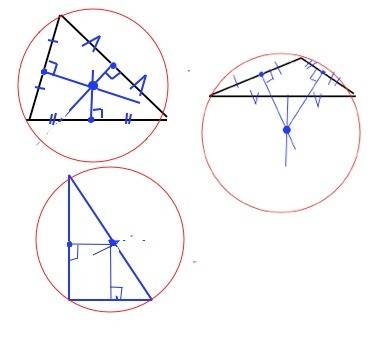
1) Для остроугольного треугольника центр описанной окружности будет внутри треугольника. .
Измерьте линейкой каждую сторону треугольника и найдите ее середину. С угольника ( у него есть прямой угол) проведите из середины каждой стороны прямые. Точка их пересечения - искомый центр описанной окружности.
Расстояние от него до вершин треугольника равны радиусу описанной окружности.
2) Для тупоугольного треугольника построение будет таким же, но срединные перпендикуляры пересекутся ВНЕ треугольника.
3) Для прямоугольного треугольника достаточно найти середину гипотенузы, т.к. срединные перпендикуляры пересекаются именно в этой точке. Полезно запомнить, что центром описанной вокруг прямоугольного треугольника окружности является середина его гипотенузы, т.к. расстояния от нее до вершин треугольника равны.
Как это выглядит, дано в приложении.
11 градусов
Объяснение:
начертим прямоугольный треугольник АВС так, что бы справа у него был прямой угол.
проведём из прямого угла сначала медиану, а потом биссектрису другим цветом(что б не запутаться.)
Обазначим медиану СD, а биссектрису СX
Слева будет острый угол, равный 34.
тогда по свойству прям. угол. треуг. медиана, проведённая из вершины прямого угла равна половине гипотенузы.
Отмечаем это на черчеже.
Видим, что у нас образовался р/б треугольгик АСD.
У него есть острый угол равный 34- по мусловию.
Тогда по св0ву р/б треуг. углы при основании равны.
тогда угол DCA равен 34.
Но мы знаем, что биссектриса делит прямой угол пополам.
Тогда угол ВСА : 2 равно 45 равно углы DCX и XCA.
Теперь мы вычитаем из угла XCA угол DCA равно 45-34=11 градусов
Равно угол XCD
ΔАСД: ∠Д=60° , ∠АСД=90° ⇒ ∠САД=30° .
Катет СД, лежащий против угла в 30° = половине гипотенузы АД ⇒
АД=2·СД
Если обозначим СД=а, то АД=2а.
Так как АС - биссектриса, то ∠ВАС=∠САД=30°.
∠ВАД=∠ВАС+∠САД=30°+30°=60° ⇒
∠ВАД=∠АДС ⇒ трапеция равнобедренная ⇒ АВ=СД=а .
∠САД=∠ВСА как внутренние накрест лежащие ⇒ ∠ВСА=30°.
Так как ∠ВАС=∠ВСА=30°, то ΔАВС - равнобедренный ⇒
АВ=ВС=а.
Периметр Р=АВ+ВС+СД+АД=а+а+а+2а=5а
5а=25 ⇒ а=5
АВ=ВС=СД=5 см , АД=10 см .