Пусть S₁ - это площадь бо́льшего треугольника, а S₂ - площадь меньшего треугольника.
Пусть k > 1 (это значит, что в числителе будет стоять бо́льший треугольник).
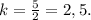
Отсюда -
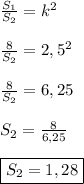
1,28 (ед²).
- - -
Случай 2 - Площадь меньшего треугольника равна 8 (ед²).В этом случае наоборот k < 1 (в числителе будет стоять меньший треугольник).
S₁ - площадь бо́льшего треугольника, S₂ - площадь меньшего треугольника
Тогда -
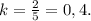
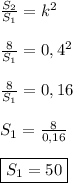
50 (ед²).

AD*BD=CD^2 (по свойству высоту прямоугольного треугольника). С другой стороны, AD+BD=13. Тогда нужно решить систему уравнений: AD+BD=13, AD*BD=36. AD=13-BD, (13-BD)*BD=36, BD^2-13BD+36=0. Тогда AD=9, BD=4, или AD=4, BD=9. Теперь из прямоугольных треугольников ACD, BCD можно по длинам двух катетов узнать длины гипоненуз AC, BC. Они равны sqrt(117), sqrt(52).