Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).
Как это получается?
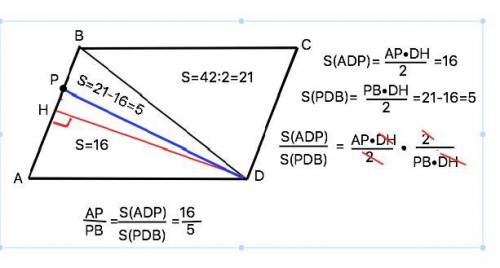
Объяснение: Диагональ ВD делит параллелограмм площадью 42 ед. на два равных треугольника. Площадь каждого 42:2=21 ед.
Ѕ ∆ АРD = 16 ед (дано), => Ѕ ∆ РВD=21-16=5 (ед).
Треугольники АРD и РВD имеют общую высоту DH. Соответственно:
S(ADP)=AP•DH:2
S(PBD)=PB•DH:2 => S(ADP):S(PBD)=(AP•DH:2):(PB•DH:2) = АР:РВ =>
АР:РВ=S(ADP):S(PBD)=16:5 (см. рисунок приложения).
∠AOE = ∠EOB - 105°
∠AOE + ∠EOB = 147°
(∠EOB - 105°) + ∠EOB = 147°
2∠EOB = 147° + 105°
2∠EOB = 252°
∠EOB = 252° : 2
∠EOB = 126°
∠AOE = 126° - 105° =21
Я думаю что это так но не знаю что это правильно или нет