Даны точки A: [-12;-4] B: [-5;-6] C: [0;3] .
Координаты вектора BC: (0 - (-5); 3 - (-6)) = (5; 9).
Длина вектора AB = √((-5)² + (-12)²) = √(25 + 144)= √169 = 13.
Координаты середины отрезка AC: ((-12+0)/2=-6; (-4+3)/2=-0,5) = (-6; -0,5).
Периметр треугольника ABC.
Расчет длин сторон
АВ (с) = √((Хв-Ха)²+(Ув-Уа)²) = √53 ≈ 7,28011.
BC (а)= √((Хc-Хв)²+(Ус-Ув)²) = √106 ≈ 10,29563.
AC (в) = √((Хc-Хa)²+(Ус-Уa)²) = √193 ≈ 13,89244399.
Периметр равен Р = 31,46818.
Длина медианы BM. Точка М - середина АС:(-6; -0,5).
ВМ = √(-6-(-5))² + (-0,5-(-6))²) = √(1 + 30,25) = √31,25 ≈ 5,59017.
Чертёж смотрите во вложении.
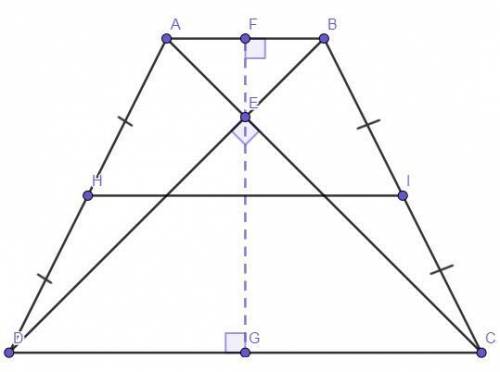
Дано:Четырёхугольник ABCD — равнобедренная трапеция (AD и ВС — боковые стороны, АВ и DC — основания).
DB и АС — диагонали.
Е — точка пересечения диагоналей.
∠DEC = 90°.
FG — высота.
НI — средняя линия = 6 см.
Найти:S(ABCD) = ?
Решение:Если у равнобедренной трапеции диагонали взаимно перпендикулярны, то высота равна средней линии.
То есть -
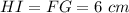
Площадь трапеции равна произведению средней линии и высоты.
То есть -
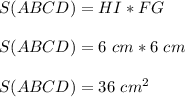
(А вообще, можно сформулировать такую теорему — Если у равнобедренной трапеции диагонали взаимно перпендикулярны, то площадь этой трапеции равна квадрату её высоты (или средней линии.)
ответ: 36 см².