Дано: А(-3; 9), В(-4; -8), С(6; 0)
Найти:
а)координаты вектора АС;
б)длину вектора ВС;
в)координаты середины отрезка АВ:
г)периметр треугольника АВС;
д)длину медианы СМ.
a) AC = {Cx - Ax ; Cy - Ay}
AC = {6 - (-3) ; 0 - 9}
AC ={9 ; -9}
б) BC = {Cx - Bx ; Cy - By}
BC = {6 - (-4); 0 - (-8)}
BC = {10 ; 8}
|BC| =  =
= 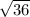 = 6
= 6
в) Пусть это будет точка M, тогда её координаты будут равны
M((Ax + Bx)/2 ; (Ay + By)/2)
M((-3 + -4)/2 ; (9 + 8)/2)
M(-3,5 ; 8,5)
г) Посчитаем длину каждой стороны треугольника
AB = 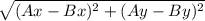 =
= 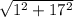 =
= 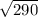
AC = 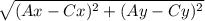 =
= 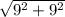 =
= 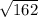
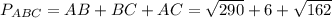
д) СМ = 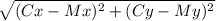 =
= 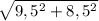 =
= 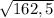
AC = 10 см.
Объяснение:
A ---D--- C --- --- B
Т.к. точка C это середина отрезка AB, то AC=CB=1/2 от общей длины отрезка AB.
Т.к. точка D это середина отрезка AC, то AD=DC = (1/2) : 2 = 1/2 : 2/1 =1/2 * 1/2 = 1/4 от общей длины отрезка AB.
Из этого следует, что BD = 1/2 + 1/4 = 2/4 + 1/4 = 3/4 части отрезка AB и равна 15 см. AB=3/4=15см.
Соответственно AD = 1/4 части
3/4 = 15
1/4 = AD
AD = 1/4 * 15 : 3/4 = 15/4 : 3/4 = 15/4 * 4/3 = 15/3 = 5 см.
AB = AD + DB = 5 + 15 = 20 см
Длина отрезка AC = 20 / 2 = 10 см.
ΔАСД - прямоугольный, ∠АСД=90° ⇒ ∠САД=90°-60°=30° ,
Против угла в 30° лежит катет, равный половине гипотенузы,
то есть СД=1/2*АД ⇒ АД=2*СД=2а (обозначим СД=а) .
∠САД=∠САВ, т.к. АС - биссектриса ⇒ ∠ВАД=30°+30°=60° ⇒
∠Д=∠А=60° ⇒ АВСД - равнобедренная трапеция, тогда АВ=СД=а .
∠САД=∠АСВ как внутренние накрест лежащие при параллельных прямых АД и ВС и секущей АС.
∠АСВ=30° и ∠ВАС=30° ⇒ ΔАВС - равнобедренный ⇒ АВ=АС=а
Периметр трапеции Р=АВ+ВС+СД+АД=а+а+а+2а=5а
5а=25 ⇒ а=5
АВ=ВС=СД=5 см , АД=10 см.