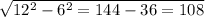
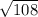
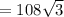
Эта задача на теорему косинусов, но для того, чтобы начать решать через теорему, нужно знать стороны. А для этого нам даны координаты. Найдем коориданты векторов AB,BC,AC. Для этого вспомним правило: чтобы найти координаты вектора, нужно из координат конца вектора, вычесть координаты начала вектора.
AB(1-0;-1-1; 2+1)=AB(1;-2;3)
BC(3-1;1+1;0-2)=BC(2;2;-2)
AC(3-0;1-1;0+1)=AC(3;0;1)
Теперь найдем длину этих векторов.
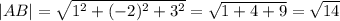
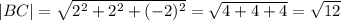
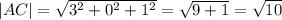
Теперь запишем теорему косинусов, используя косинус угла С.
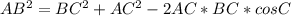
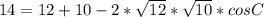
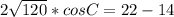
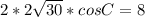
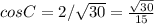
Нужно все проверить!