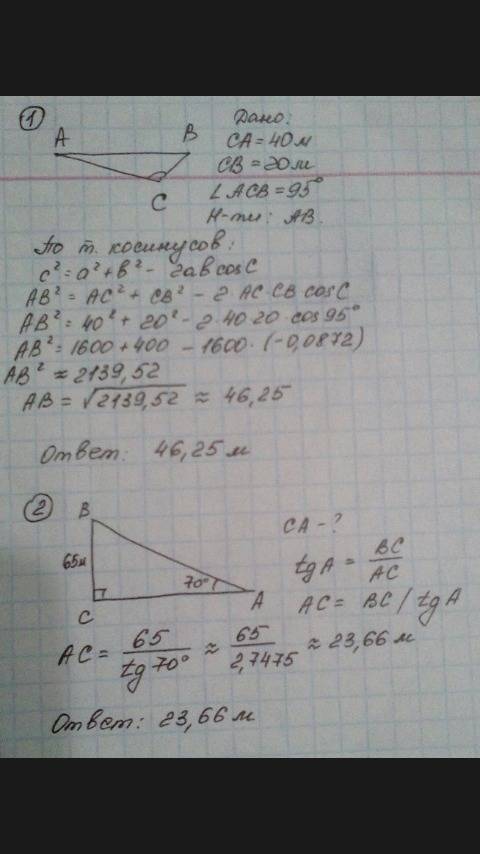
Объяснение:
Точки А и В лежат в плоскости альфа, а точки С и D- в плоскости бета, причём альфа параллельна бета, АВ=СД, а отрезки АС и ВD пересекаются.
а) докажите, что АВ параллельна СD.
б) Один из углов четырёхугольника АВСD равен 65 градусов. Найдите остальные углы
а) АС и ВD пересекаются.
Через две пересекающиеся прямые можно провести плоскость, и притом только одну; то же справедливо и для параллельных прямых.
Следовательно, прямые АВ и СD лежат в той же плоскости. что АС и ВD.
Проведем из D и В перпендикуляры кD и Ве к противоположной плоскости.
Т.к. плоскости α и β параллельны, то кD и Ве параллельны и равны ( на основании того, что это - перпендикуляры между параллельными плоскостями)
Прямые кВ и Dе лежат в одной плоскости кВeD, расстояние между ними равно, следовательно, они параллельны.
АВ принадлежит кВ, DС принадлежит Де, следовательно, АВ||СD.
б) Четырехугольник, в котором противоположные стороны равны и параллельны, - параллелограмм.
Противоположные углы параллелограмма равны.
Сумма углов, прилежащих к одной стороне параллелограмма, равна 180°
Острые углы четырехугольника АВСD равны по 65°. Тупые по-180-65=115°———
Пусть ABC - равнобедренный
∟B = 120 °, АС = 18 см, АК - высота.
В ΔАВС проведем высоту BD к основанию АС.
По свойству равнобедренного треугольника BD - биссектриса и медиана
AD = DC = 1 / 2AC = 18: 2 = 9 (см) (BD - медиана).
∟AВD = ∟DBC = 1 / 2∟В = 120 °: 2 = 60 ° (BD - биссектриса).
Рассмотрим ΔABD - прямоугольный (∟D = 90 °, BD - высота):
∟BAD + ∟ABD = 90 °; ∟BAD = 30 °; ∟BAD = ∟BCD = 30 ° (ΔABC - равнобедренный).
Рассмотрим ΔАКС (∟К = 90 °, АК - высота):
АК - катет, лежащий напротив угла 30 °, тогда АК = 1 / 2АС; АК = 18: 2 = 9 (см).
ответ: Высота AK= 9 см