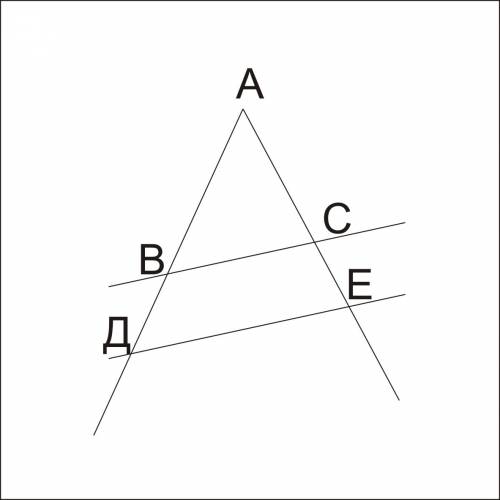
По условию ∆ АВС -равносторонний, боковые стороны равны 12, а диаметр основания равен 10•2=20. Следовательно, АВС не является осевым сечением конуса. Соединим центр О основания с А и С.
Треугольник АОС равнобедренный, АС=L=12 (из условия); высота ОК делит его на два равных прямоугольных треугольника с гипотенузой, равной R=10, и катетами АК=АС:2=6 и ОК (его длину нужно найти).
Отношение АК:ОА=6:10=3:5, следовательно, ∆ АОК "египетский, его катет ОК=8 ( можно найти по т.Пифагора)
Высота ВО конуса перпендикулярна основанию и проецируется в его центр. ∆ ВОС - прямоугольный. Катет ОС=R=10, гипотенуза ВС=12.
По т.Пифагора ВО=√(ВС²-ОС²)=√(144-100)=2√11
АЕ-бісектриса кута А
ВЕ БІЛЬШИЙ ЗА ЕС в 3 раза
ВС=12 см
Знайти:Р-?
РОЗВЯЗАННЯ
Нехай ЕС=х см, тоді ВЕ=3х.ВС=ЕС+ВЕ=12.Тому маємо рівняння:
х+3х=12
4х=12
х=3 - ЕС
ВЕ=3*3=9
ВС=AD=12см
Нехай сторона СD=х, тоды й сторона АВ=х
х+х=24
2х=24
х=12
Р=12*4=24 тому це квадрат.
(Я ДУМАЮ ЩО ТАК)