500
Объяснение:
Sтрапеции = (а+b)/2·h, где а и b - основания, а h - высота.
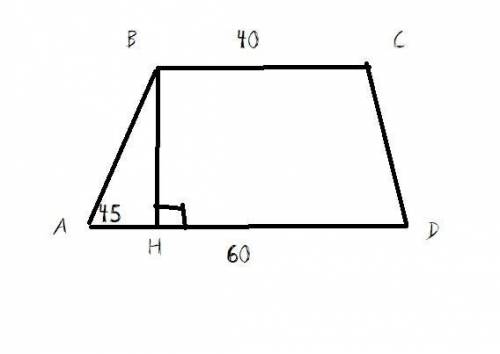
Основания мы знаем, нужно провести и найти высоту. Проводим высоту BH.
Рассмотрим треугольник АBH. Один из его углов равен 45° (по условию), другой угол равен 90° (так как BH высота). Значит, ∠ABH = 180-90-45 = 45°. Два угла треугольника равны по 45° - значит, треугольник равнобедренный. Значит, стороны BH и АH равны.
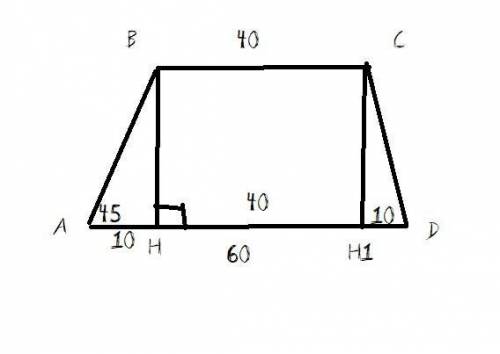
Проведем еще одну высоту CH1. Получаем прямоугольник HBCH1. В нем ВС = HH1 = 40 => АН и Н1D равны по 10.
Если АН равно 10, то и BH (высота) равно 10.
S трапеции = (40+60)/2·10 = 100/2·10 = 50·10 = 500
пусть AB=13 AC=37
A1B - проекция AB=k
A1C - проекция AC=7k
треугольники AA1B u AA1C прямоугольные. запишем т.Пифагора для каждого:
AB^2=AA1^2+A1B^2
AC^2=AA1^2+A1C^2
выражаем квадрат стороны АА1( т.е. перпендикуляр от точки к плоскости, длина которого и будет искомым расстоянием от плоскости до точки):
AB^2-A1B^2=AC^2-A1C^2
13*13-k*k=37*37-49*k*k
k^2=25
подставляем k^2:
АА1=AB^2-A1B^2=169-25=144
AA1=12 (AA1=-12 не подходит, т.к. расстояние величина неотриц.).
ответ: 12