6 ед.
Объяснение:
В правильной усеченной пирамиде в основаниях лежат правильные многоугольники, стороны которых соответственно равны между собой. Боковые грани такой пирамиды - равные между собой равнобокие трапеции. Радиусы окружностей, вписанных в основания, проведенные в точки касания сторон оснований с соответственной окружностью Н и Н1, перпендикулярны к сторонам оснований по свойству радиусов, проведенных в точки касания.
Проведем перпендикуляр из точки касания Н1М верхнего основания на нижнее основание. Тогда отрезок Н1Н перпендикулярен стороне основания АВ по теореме о трех перпендикулярах, то есть является искомой высотой боковой грани.
В прямоугольном треугольнике НН1М угол ∠НН1М = 30° по сумме острых углов. Следовательно, НН1 = 2·НМ по свойству катета, лежащего против угла 30°.
НМ = ОН - О1Н1 = 8-5 = 3 ед.
Высота боковой грани НН1 = 6 ед.
 с прямым углом
с прямым углом  , EF — биссектриса
, EF — биссектриса  ,
,  , FG — искомый отрезок.
, FG — искомый отрезок.  .
.  — биссектриса, то
— биссектриса, то  (биссектриса
(биссектриса  делит
делит  на два равные угла).
на два равные угла). 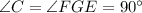 (это следует из условия: так как
(это следует из условия: так как  прямоугольный, то и
прямоугольный, то и  ; так как
; так как  — расстояние от
— расстояние от  до
до 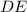 , то
, то 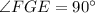 ).
).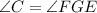 и
и 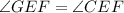 , то и третий угол первого треугольника равен третьему углу второго треугольника:
, то и третий угол первого треугольника равен третьему углу второго треугольника:  . Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так:
. Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так: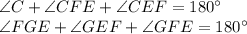
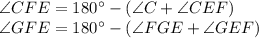
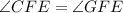 .
.  является для обоих треугольников общей.
является для обоих треугольников общей. (второй признак равенства треугольников — по стороне и двум прилежащим к ней углам (
(второй признак равенства треугольников — по стороне и двум прилежащим к ней углам ( — сторона, а
— сторона, а  — два прилежащих угла)).
— два прилежащих угла)). соответствует
соответствует  , тогда:
, тогда: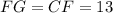
 . Смотрите второй рисунок.
. Смотрите второй рисунок.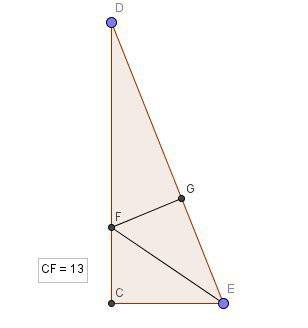
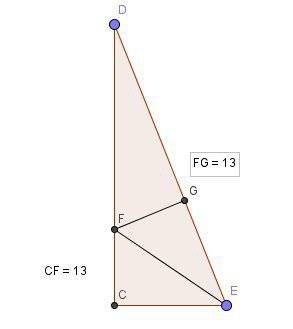
17-7=10(гипотенуза)
7:2=3,5см(катеты)