Приведите примеры векторных величин, известных вам из курса физики.
Ускорение (а), скорость (V), ускорение свободного падения (g).
Дайте определения вектора. Объясните, какой вектор называется нулевым.
Вектор - это отрезок имеющий направление. Вектор называется нулевым, если его начало совпадает с его концом, (т.е. длина 0)
Что называется длиной ненулевого вектора? Чему равна длина нулевого вектора?
Длина ненулевого вектора не равна 0, и его начало не совпадает с его концом. Длина нулевого вектора равна 0.
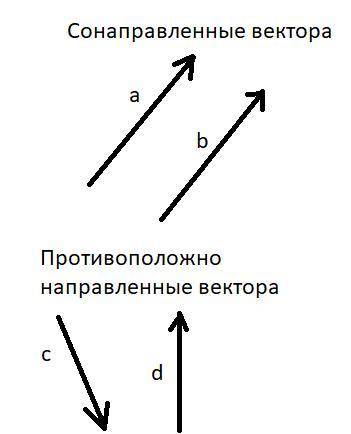
Какие вектора называются коллиниарными? Изобразите на рисунке сонаправленные вектора a и b и противоположно направленные вектора c и d.
Вектора коллинеарны, если они параллельны, (или лежат на одной плоскости).
Дайте определения равных векторов.
Вектора равны, если они сонаправлены и их длины равны.
Только так, не забудь на рисунке вектора над буквами подписать
Основания - правильные треугольники. О₁ - центр верхнего основания (точка пересечения медиан (биссектрис, высот)), О - центр нижнего основания.
Пусть Н - середина В₁С₁, тогда О₁Н - радиус окружности, вписанной в треугольник А₁В₁С₁.
О₁Н = а√3/6 = 6√3/6 = √3 см
Пусть К - середина ВС, тогда ОК - радиус окружности, вписанной в треугольник АВС:
ОК = 12√3/6 = 2√3 см.
ОО₁ - высота пирамиды, тогда
ОО₁⊥ВС и АК⊥ВС, т.е. ребро ВС перпендикулярно двум пересекающимся прямым плоскости АКН, значит
ВС⊥(АКН)
Тогда ВС⊥КН, ∠НКА = 30° и НК - апофема пирамиды.
Sбок = (P₁ + P₂) · HK, где P₁ и P₂ - периметры оснований.
Осталось найти НК.
ОО₁НК - прямоугольная трапеция. Проведем в ней высоту НТ.
ОО₁НТ - прямоугольник, ОТ = О₁Н = √3 см
ТК = ОК - ОТ = 2√3 - √3 = √3 см
ΔНТК: cos 30° = TK / HK
HK = TK / cos 30° = √3 / (√3/2) = 2 см
Sбок = (P₁ + P₂) · HK = (6 ·3 + 12 · 3) · 2 = (18 + 36) · 2 = 54 · 2 = 108 см²
Т.е сумма оснований есть 14+14=28
Всего частей 3+4=7, чтобы найти одну часть 28:7=4
Соответственно меньшее основание
12
Большее основание 16