28 см²
Объяснение:
Дано:
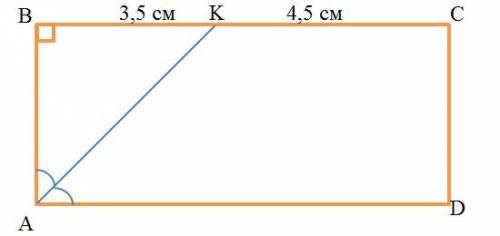
Прямоугольник ABCD (см. рисунок)
AK – биссектриса:
∠KAB = ∠KAD, K∈BC
BK=3,5 см
KC=4,5 см
Найти: площадь прямоугольника S(ABCD).
Решение: У прямоугольника ABCD все углы равны, поэтому ∠B=∠A=90°.
Так как AK – биссектриса, то ∠KAB=90°:2=45°.
Следовательно, как внутренний угол треугольника
∠BKA=180°–∠B–∠KAB= 180°–90°–45°=45°.
Тогда, так как углы при основании треугольника AKB равные, то треугольник AKB равнобедренный: AB=BK=3,5 см.
Имеем: BC=BK+KC=3,5 см+4,5 см=8 см.
Теперь можем определить площадь прямоугольника
S(ABCD)=AB•BC= 3,5 см • 8 см = 28 см².
<X=40°
Объяснение:
∆ВАD- равнобедренный треугольник.
В равнобедренном треугольнике углы при основании равны
<В=<АDB
Сумма углов в треугольнике равна 180°
<B=(180°-<BAD)/2=(180°-70°)/2=110°/2=55°
∆ВАС.
Сумма углов в треугольнике равна 180°
<ВАС=180°-<В-<С=180°-55°-45°=80°
<DAC=<BAC-<BAD=80°-70°=10°
∆DAE- равнобедренный.
В равнобедренном треугольнике углы при основании равны.
<АDE=<AED
<AED=(180°-<DAE)/2=(180°-10°)/2=85°
<AED- внешний угол треугольника ∆DEC.
Теорема о внешнем угле треугольника: внешний угол треугольника равен сумме внутренних углов треугольника не смежных с ним.
<ЕDC+<ECD=<AED
<EDC=<AED-<ECD=85°-45°=40°
<X=40°
трапеция прямоугольная, значит 2 угла другие равны 90+90=180
180+х+3х=360°
4х=360-180
4х=180°
х=45° меньший угол
3х=135° больший угол