Объяснение: - - - - - - - задание N 1 - - - - - - -
- Центр окружности, вписанной в тупоугольный треугольник ,находится вне треугольник ← (неверно)
- - - - - - - задание N 2 - - - - - - -
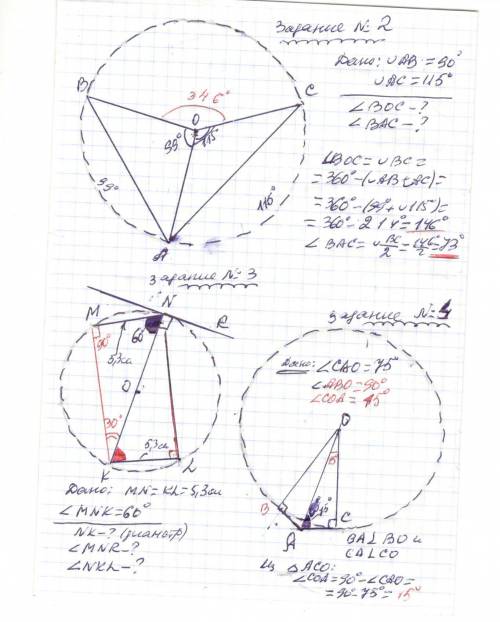
◡ BC = 360° -(◡AB + ◡AC) =360° -( 99°+ 115°) =360° -214° = 146°
∠BOC = ◡ BC = 146° как центральный угол
∠BAC = ◡ BC/2 = 146°/2 = 73° как вписанный угол
- - - - - - - задание N 3 - - - - - - -
KN ⊥ NR ( NR касательная окружности в точке касания N )
NK диаметр ⇒ ∠NMK = 90° (вписанный угол опирающий на диаметр)
В прямоугольном треугольнике NMK :
∠MKN = 90° - ∠MNK = 90° - 60° = 30°
MK =NK/2 ( как катет против угла 30° ) ⇒ NK =2*MK =2*5,3 см =10,6 см
∠MNR = ∠MNK+∠KNR =60°+90° =150° .
ΔKLN = ΔNMK ( по гипотенузе и катету)
следовательно ∠NKL = ∠ KNM = 60° .
* * * * NMKL прямоугольник * * *
- - - - - - - задание N 4 - - - - - - -
BA ⊥ BO , CA ⊥ cO
∠ABO = 90° , ∠ACO = 90°
Из ΔACO: ∠COA = 90° - ∠CAO = 90° - 75° =15° рис. см приложение
В ∆ АВС высоты АА1 и СС1 со сторонами два прямоугольных треугольника АС1С и АА1С с общей гипотенузой АС.
Следовательно, вокруг них можно описать окружность с диаметром АС, на который опираются прямые углы АС1С и АА1С.
Вписанные углы А1АС и А1С1С опираются на одну дугу А1С. Вписанные углы, опирающиеся на одну дуга, равны. ⇒
∠СС1А1=∠САА1. Доказано.
Рассмотрим ∆ АОС1 и А1ОС.
Эти треугольники подобны по двум углам - прямому при С1 и А1 и вертикальному при точке пересечения высот О.
Из подобия следует пропорциональность сторон:
С1О:А1О=АО:СО,
откуда имеем пропорциональность тех же сторон в ∆ АОС и ∆ А1ОС1.
Вертикальные углы при вершине О этих треугольников равны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Следовательно, углы СС1А1 и САА1 равны. Доказано.
Объяснение: