S BB₁C₁C = ?
Работаем с 3-мя прямоугольниками. ABCD, ADC₁B₁, BCC₁B₁
Обозначим: АВ = CD = a, BC = AD = b, CC₁ = x
S BB₁C₁C = хb
SABCD = 12 = ab
SADC₁B₁ = 20 = b*DC₁ ( DC₁ ищем по т. Пифагора из ΔCDC₁
DC₁ = √(x² + a²)
20 = b*√(x² + a²)
рассмотрим систему уравнений:
20 = b*√(x² + a²)
12 = ab
Разделим 1-е уравнение на 2-е. Получим:
20/12 = √(x² + a²)/а, ⇒ 5/3 = √(x² + a²)/а | ², ⇒ 25/9 = (x² + a²)/а², ⇒
⇒25а² = 9(х² + а²), ⇒ 25а² = 9х² + 9а², ⇒16а² = 9х², ⇒ х² = 16а²/9, ⇒
⇒ х = 4а/3
Теперь смотрим S BB₁C₁C = хb = 4a/3*b = 4ab/3 = 4*12/3 = 16
ответ : S BB₁C₁C = 16см²
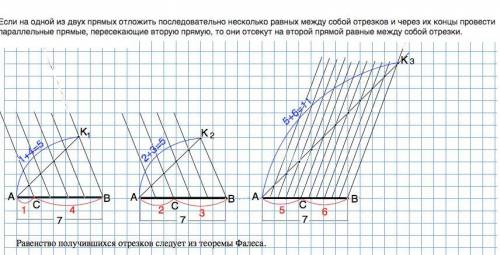
Объяснение (подробно):(см. рисунок приложения.)
Чертим отрезок АВ=7 см. Из А проведем луч и отложим на нем равные отрезки заданным числом. Конец последнего отрезка соединим с концом В заданного отрезка. Через концы отложенных на луче отрезков проведем прямые, параллельные прямой ВК. (Если не помните, как провести прямую, параллельную данной, найдите в учебнике, и в интернете на эту тему много информации).
а) на проведенном луче отложим 1+4=5 равных отрезков. Прямые, параллельные К1В, делят АВ на 5 равных частей. Часть АС=1, часть СВ=4. Длину получившихся отрезков можно посчитать на калькуляторе.
АС=7:5•1 (см); СВ=7:5•4(см)
б) отрезок АВ тем же делим на 2+3=5 частей.
АС=7:5•2 (см); СВ=7:5•3 (с м)
в) аналогично на проведенном луче отложим 5+6=11 равных частей, и отрезок АВ делится на 11 равных частей.
АС=7:11•5 (см); СВ=7:11•6 (см)