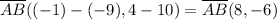 ;
; от точки A
от точки A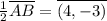 ;
; в обе возможные стороны
в обе возможные стороны перпендикулярен вектору основания
перпендикулярен вектору основания  , а значит его проекции накрест-пропорциональны с противоположным знаком:
, а значит его проекции накрест-пропорциональны с противоположным знаком: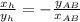 , что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:
, что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:  (II) ;
(II) ; пропорционален вектору
пропорционален вектору  , поскольку для вектора
, поскольку для вектора  выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора
выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора  ;
; имеет длину
имеет длину 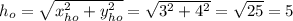 ;
;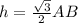 , т.к
, т.к 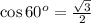 ;
;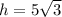 , а стало быть
, а стало быть  ;
;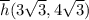 .
.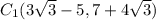 /// примечание:
/// примечание: 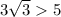 ;
;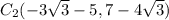 /// примечание:
/// примечание: 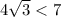 .
.
Радиус вписанной окружности основания
r = √3/6·a
Радиус описанной окружности
R = √3/3·а
Площадь основания
S = √3/4·a²
а) Сечение параллельно основанию через середину высоты.
Треугольник этого сечения подобен треугольнику основания с коэффициентом подобия k = 0,5
Площадь сечения относится с площадью основания как k²
s₁ = S·k² = S/4 = √3/16·a²
б) Сечение проходит через боковое ребро и высоту
Основание треугольника сечения r+R, высота h
Площадь
s₂ = 1/2(r+R)h = 1/2(√3/6·a+√3/3·a)h = 1/2√3/2·ah = √3/4·ah
в) сечение через сторону основания перпендикулярно противоположному боковому ребру
В треугольнике из пункта и в текущем высота h₃ общая (на рисунке синяя). Найдём ей через площадь треугольника из пункта.
Нам нужна длина бокового ребра пирамиды
l² = h²+R² = h²+a²/3
l = √(h²+a²/3)
s₂ = 1/2 h₃l
√3/4·ah = 1/2 h₃√(h²+a²/3)
√3/2·ah = h₃√(h²+a²/3)
h₃ = √3·ah/(2√(h²+a²/3))
s₃ = 1/2·h₃a = √3·a²h/(4√(h²+a²/3)) = 3a²h/(4√(3h²+a²))
г) сечение через центр основания параллельно боковой грани
Треугольник этого сечения параллелен и подобен боковой грани пирамиды с коэффициентом подобия k = R/(R+r) = 2/3
Найдём плошадь боковой стороны
Её высота (синяя)
l² = h²+r² = h²+3/36·a² = h²+a²/12
l = √(h²+a²/12)
площадь боковой стороны
s = 1/2·al = 1/2·a√(h²+a²/12)
площадь сечения
s₄ = k²s = 4/9·1/2·a√(h²+a²/12) = 2/9·a√(h²+a²/12)
д) Сечение через середины четырех ребер
Такое сечение можно построить только проходящим через середины двух рёбер основания и двух боковых рёбер
Сечение имеет форму четырёхугольника (или равносторонняя трапеция или прямоугольник)
Нижнее ребро b₁ - средняя линия основания, его длина
b₁ = a/2
Боковое
b₂ и b₄ - средняя линия боковой грани и в два раза короче бокового ребра, длину его вычисляли раньше √(h²+a²/3)
b₂ = b₄ = (√(h²+a²/3))/2
верхнее ребро b₃ - средняя линия боковой грани, проведённая параллельно основанию, его длина
b₃ = a/2
Итого - у нас прямоугольник с площадью
s₅ = a/2·(√(h²+a²/3))/2 = (a√(h²+a²/3))/4