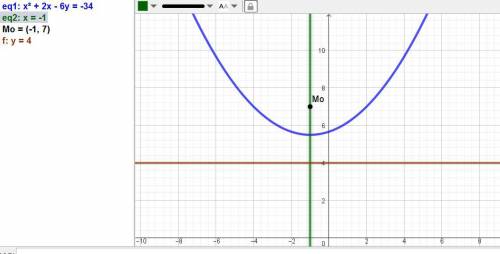
Заданное ГМТ соответствует параболе - это геометрическое место точек плоскости, равноудаленных от заданной точки F и заданной прямой d, не проходящей через заданную точку.
Поэтому точка Мо и есть фокус параболы, а прямая у = 4 её директрисой.
Расстояние от фокуса до директрисы равно параметру параболы "р" и равно 7 - 4 = 3.
Вершина параболы находится посередине между фокусом и директрисой. Для нашей задачи получаем координаты вершины:
(-1; 5,5).
Так как директриса параллельна оси Ох, то ось параболы параллельна оси Оу. Уравнение (x-xо)^2=2p(y-yо), p > 0 определяет параболу с вершиной O'(xo,yo), ось которой параллельна оси ординат.
Все данные для уравнения мы определили.
ответ: уравнение параболы (x + 1)² = 2*3(y - 5.5).
Р = 27 см.
Объяснение:
Так как треугольник равнобедренный, то две его стороны (боковые) равны. В условии не сказано, какая из двух данных нам разных по длине сторон боковая. Следовательно, мы должны проверить два варианта решения.
Первый вариант: пусть основание равно 11 см. Тогда боковые стороны равны по 5 см. Но это противоречит теореме о неравенстве треугольника, по которой большая из трех сторон треугольника должна быть меньше суммы двух других сторон: 11 > (5+5). Значит этот вариант решения не удовлетворяет условию существования треугольника.
Второй вариант: пусть основание равно 5 см. Тогда боковые стороны равны по 11 см. => 11 < (11+5) => условие существования треугольника выполняется. Следовательно, такой треугольник существует и его периметр (сумма всех сторон) равен Р = 11+11+5 = 27 см.