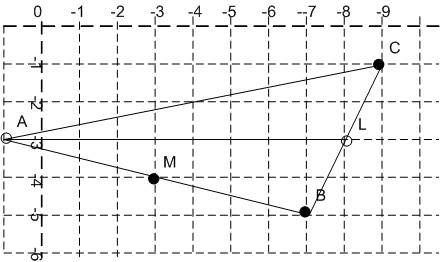
Первое решение - геометрическое.
Строим на тетрадном листике координаты и чертим точки с известными координатами. Так как нам известно, что точи М и L - середины отрезка, то доводим линию BM до точки A и видим, что он оказывается в координатах A(1,-3). Также по чертежу видно, что координаты L(-8.-3). По чертежу выйдет, что AL - прямая линия и ее длина составляет 9 клеток.
Решение по формулам
У нас есть B и С - точка середины отрезка L вычисляется по формуле
L = (B+C)/2.
Lx = (-7 + -9)/2 = -8; Ly= (-5 + -1) / 2 = - 3.
Координаты L(-8.-3).
Если подумать, то отрезок AB с точкой M - тоже вычисляется по этой же формуле:
M = (A + B) / 2.
Отсюда A = 2M - B
Значит
Ax = (2 * (-3)) - (-7) = +1
Ay = (2 * (-4)) - (-5) = - 3
Точка A(1,-3)
Длина отрезка AL = квадратный корень из ((Ax - Lx) ^2 + (Ay - Ly)^2))
AL =квадраткорень( (1- (-8))*(1- (-8)) + (-3- (-3))* (-3- (-3)) = квадраткорень (9*9 - 0*0) = 9
Как-то так.
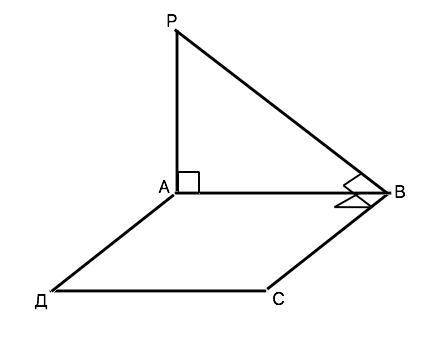
РА - перпендикуляр к площади параллелограмма АВСД. Укажите вид параллелограмма, если РВ перпендикулярен ВС. а) ромб, б) прямоугольник; в) квадрат.
Объяснение: РВ - наклонная. АВ - её проекция на плоскость АВСД. По т. о 3-х перпендикулярах если наклонная (РВ) перпендикулярна прямой (ВС) на плоскости, то её проекция на ту же плоскость перпендикулярна данной прямой. Следовательно, АВ⊥ВС, и угол АВС - прямой. Противоположные углы параллелограмма равны. ⇒ ∠Д=∠В=90°, поэтому из суммы углов четырехугольника ∠А+∠С=360°-2•90°=180°, и каждый из них равен 180°:2=90°.
Углы четырехугольника АВСД прямые. ⇒ АВСД - прямоугольник. Он может быть и квадратом. если его стороны будут равны.
Плоскость α параллельна АС (α|| AC) - дано.
Значит и линия пересечения MN || AC.
Две параллельные прямые AC и MN и секущая АВ.-
∠ВАС = ∠BMN
∠BCA = ∠BNM
ΔABC ~ ΔAMN - подобные.
Коэффициент подобия - k = AM : AB = 1/2.
AM = MB - дано. Значит и AN = NC и MN = AC/2
MN - средняя линия.
2. Треугольники АВС и А1ВС1 - подобные.
Коэффициенты подобия - k = A1C1 : AC = 6 : 9 = 2/3
Такое же отношение и у других пар сторон.
A1B : AB = C1B : CB = 2/3