1) в равностороннем треугольнике все высоты равны.
Верно.Это свойство высот равностороннего треугольника
2)точка пересечения медиан произвольного треугольника - это центр окружности, описанной около этого треугольника.
Неверно. Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника
4)медиана, это отрезок соеденяющий середины двух сторон треугольника.
Неверно. Медиана - отрезок, соединяющий вершину треугольника с серединой противоположной стороны
5) треугольник со сторонами 6,8,9- не существует.
Неверно. Существует.
Треугольник существует только тогда, когда сумма любых двух его сторон больше третьей.
Проверим:
6+8>9, 14>9
8+9>6, 17>6
6+9>8, 15>8
6) треугольник со сторонами 3,4,5 -прямоугольный.
Верно. Он египетский.
Египетский треугольник - прямоугольный треугольник с соотношением сторон 3:4:5
ответ 1 и 6
ЗАДАНИЕ 1
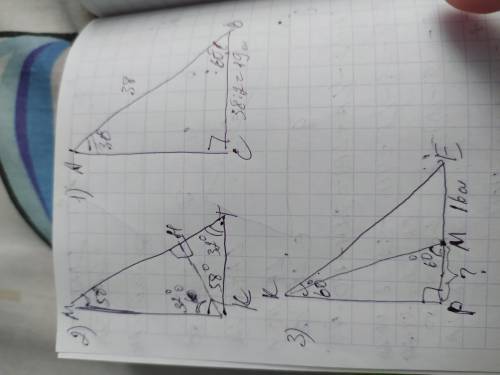
В прямоугольном треугольнике сумма острых углов составляет 90°, тогда <А=90-60=30°. Катет лежащий напротив него равен половине гипотенузы поэтому ВС=38/2=19см
ОТВЕТ: ВС=10см
ЗАДАНИЕ 2
Высота КН делит ∆КМТ на 2 прямоугольных треугольника МКН и КТН. Рассмотрим полученный ∆КМН. В нём <МКН=32° и так как сумма острых углов прямоугольного треугольника составляет 90°, то <М=90-32=58°. Также в ∆КМТ, <Т=90-58=32°.
ОТВЕТ: угол Т=32°
ЗАДАНИЕ 3
Сторона КМ образует с катетом МР <КМР=60° и ещё один прямоугольный треугольник КМР. Сумма острых углов прямоугольного треугольника составляет 90°, поэтому <МКР=90-60=30°
Также в ∆РКЕ <Е=90-60=30°.
<МКР=<Е=30°, а катет лежащий напротив него равен половине гипотенузы, поэтому КЕ=2×КР; КМ=2×РМ
Пусть РМ=х, тогда КМ=2х. Найдём КР по теореме Пифагора:
КР²=КМ²-РМ²=(2х)²-х²=4х²-х²=3х²
КР=√3х². Рассмотрим ∆РКЕ. Так как КЕ=2×КР, то КЕ=2√(3х²)
Если РМ=х, тогда РЕ=16+х
Составим уравнение используя теорему Пифагора:
КР²+РЕ²=КЕ²
(√3х²)²+(16+х)²=(2√(3х²))²
3х²+256+32х+х²=4×3х²
4х²+32х+256=12х²
4х²-12х²+32х+256=0
-8х²+32х+256=0 |÷(-8)
х²-4х-32=0
Д=16-4(-32)=16+128=144
х1=(4-12)/2= -8/2= –4
х2=(4+12)/2=16/2=8
х1 = –4 нам не подходит поскольку сторона не может быть отрицательной поэтому используем х2=8
х=РМ=8см
ОТВЕТ: РМ=8см
ответ:,32 см