ответ угол NAM = 33
Объяснение:
Рассмотрим треугольник ABC
1) Углы при основании в равнобедренном треугольнике равны, следовательно угол A = углу B = (180 - 16) : 2 = 82
2) так как AN - биссектриса, следовательно угол BAN = углу NAC = 82 : 2 = 41
Рассмотрим треугольник ABN
1) Угол BAN = 41, угол B = 16, следовательно угол BNA = 180 - 41 -16 = 123
Угол ANM = 180 - 123 = 57, так как являются смежными
Рассмотрим треугольник ANM
1) угол ANM = 57, угол AMN = 90, так как AM - высота, следовательно угол NAM = 180 - 90 - 57 = 33 градуса
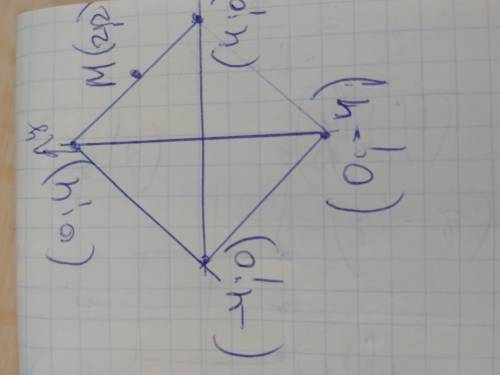
(4;0), (-4;0), (0;-4),(0;4)
Объяснение:
Оси координат - оси симметрии квадрата, но у квадрата возможны 4 оси симметрии. Это либо средние линии, либо диагонали. Т.к. Середина одной из сторон т.М(2;2), то оси симметрии - не средние линии, а диагонали, иначе середина стороны лежала бы на одной из осей и имела в координатах ноль. Значит ось х и у проходят через диагонали квадрата. Если половина значения х вершины =2, то х вершины =4, половина значения у вершины =2, то у вершины =4.
Вершинами квадрата являются точки (4;0), (-4;0), (0;-4),(0;4)
Треугольник A1BC1– равносторонний, Проведем высоту ВК (К– точка пересечения диагоналей) B1D пересекается с КВ в точке М.
Треугольники КВ1М и DBM подобны по двум углам. (см. рисунок) D1B1=DB=√2 KB1=√2/2 По теореме Пифагора B1D=√3 KB=√(3/2) KM:MB=1:2 KM:((√3/2)–KB)=1:2 KB=√6/6 B1M:MD=1:2 B1M:(√3– B1M)=1:2 B1M=√3/3
В треугольнике В1КМ B1K²=B1M²+MK² 1/2=(1/3)+(1/6) Треугольник прямоугольный угол B1MK– прямой
Итак, B1D– перпендикулярна двум пересекающимся прямым А1С1 и BK, значит перпендикулярна плоскости А1ВС1.