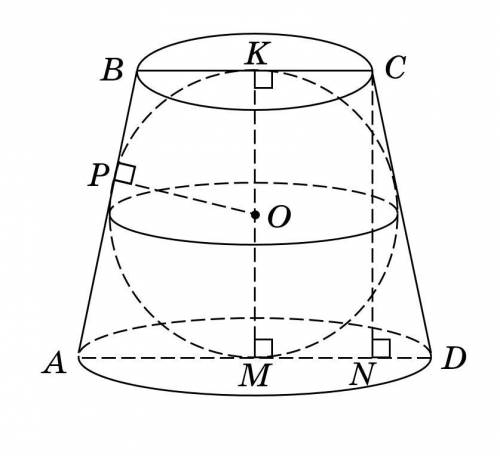
Пусть шар с центром в точке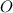 
и радиусом 
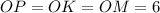см вписан в усеченный конус, у которого радиусы оснований относятся как 
.
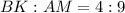Пусть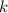 
— коэффициент пропорциональности. Тогда 
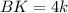, а 
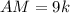
По свойству касательных: отрезки касательных проведенных из одной точки, равны. Значит,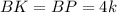 
и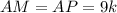 
.
Проведем высоту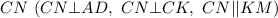 
Тогда четырехугольник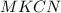 
является прямоугольником со сторона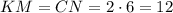ми 
см и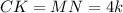 
Следовательно, катет прямоугольного треугольника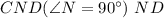 
равен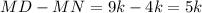 
Если трапеция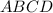 
равнобокая значит,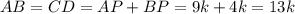 
Рассмотрим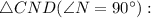 
По теореме Пифагора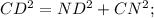 
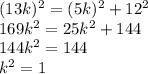
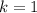
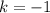— не удовлетворяет условию задачи
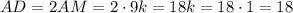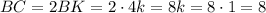см
см
Площадь осевого сечения конуса — это площадь трапеции
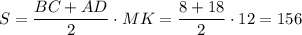см²
ответ: 156 см²
