1.
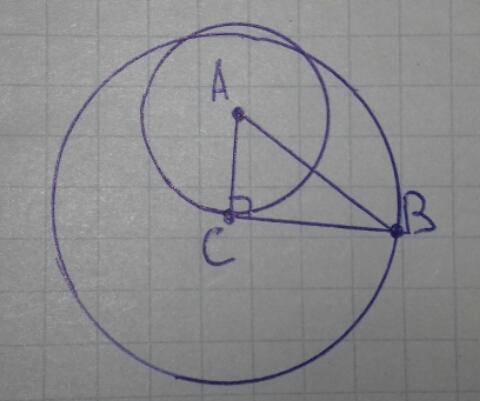
BC⊥AC как катеты прямоугольного треугольника.
BC∩AC = C; AC - радиус окружности с центром A.
Получаем, что BC перпендикулярно радиусу (AC) окружности с центром A и BC пересекает этот радиус в точке (C), принадлежащей той же окружности, поэтому BC это касательная.
2.
AB пересекает окружность (C, CB) в точке B, а CB это радиус той же окружности, проведёный к точке B. Если AB было бы касательной, то AB⊥BC, но это не возможно т.к. AB - гипотенуза, а BC - катет одного прямоугольного ΔABC. Поэтому AB не может быть касательной.
1)Тк равнобедренная трапеция, значит, углы при основаниях равны (основания - те стороны что параллельны в трапеции)
значит, сумма 2х углов = 180(град) (2а+2б=360град)
а=б +40 из условия задачи ==> а+б=180 => б+б+40=180 => 2б=140 => б=70 град
а=б+40=110град
ответ 70 и 110 градусов
2) сумма 2х соседних углов паралеллограма = 180 градусов тк по определению. стороны попарно в нем параллелльны. Диагональ БД образует со сторонами БС и БА углы 65 и 50 град ==> угол Б = 65+50 = 115 град
угол А = 180- угол Б (тк два соседних угла в параллелограме)
А = 180-165 = 15 град
ответ: 15 град
3)пусть у прямоугольника стороны а и б
тогда периметр его равен 2а+2б = 60
пусть а=12 (наименьшая сторона) тогда 2*12+2б=60 => 2б=60-24=36 => б=18(см)
ответ : 18 см
х+х+х+4+х+4=24
4х+8=24
4х=16
х=4
AD=4 BC=4 AB=8(x+4=4+4=8) DC=8
т.к. диагонали пересекаются в точке О(так обозначим точку пересечения) в центре прямоугольника, опускаем перпендикуляр на сторону DC(этим мы доказываем, что пересекаются в центре) и получается, что они пересекаются в середине большой стороны прямоугольника, а середина прямоугольника - это 8\2=4см. т.е. расстояние от точки О до сторон АD и ВС равна 4 см.