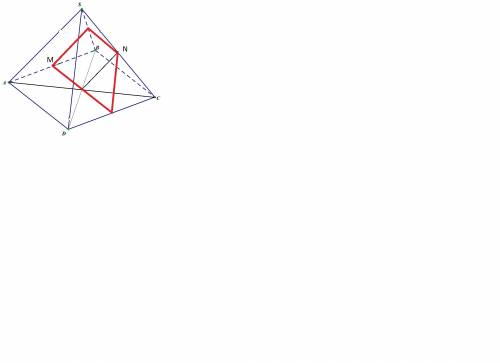
1) Так как по заданию дана правильная четырехугольная пирамида с равными рёбрами, то боковые грани такой пирамиды - это равносторонние треугольники.
Из точки N проводим прямую, параллельную SA, до пересечения с плоскостью основания. В треугольнике ASC это средняя линия, точка пересечения прямой из точки N - это центр основания, точка О.
Через точки М и О проводим след сечения заданной плоскости с основанием. Этот след пересекает ребро СД в его середине - в точке К.
Так как отрезок МК параллелен ВС (это линия пересечения боковой грани BSC и основания, то в грани BSC из точки N проводим прямую, параллельную ВС. Отрезок NP - это след сечения заданной плоскостью грани BSC.
Осталось соединить точки М и Р и сечение готово.
Оно представляет собой равнобокую трапецию. Основание её равно стороне основания пирамиды, а остальные стороны трапеции как средние линии треугольников боковых граней равны половине стороны основания.
2) Угол между прямыми SA и MN найдём методом параллельного переноса.
Перенесём отрезок MN точкой М в точку А, то есть на половину стороны основания. Тогда точка N при сдвиге на половину стороны основания переместится в середину бокового ребра CSD (на длину средней линии этой грани). Получим медиану треугольника АSD.
Так как боковая грань - равносторонний треугольник с углами по 60 градусов, то угол между ребром SA и медианой этой грани равен 30 градусов.
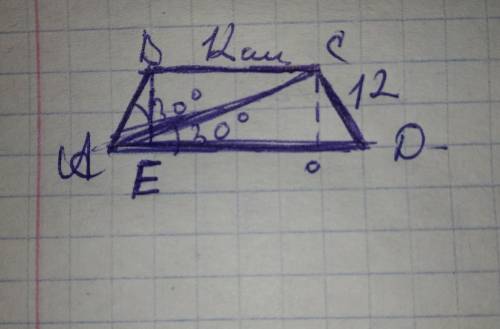
1. Площадь равнобедренного треугольника можно найти по формуле герона, так как все стороны даны: S = p(p-a)(p-b)(p-c) и все это под корнем p - полупериметр! отсюда равно = 48.
2. Площадь параллелограмма находится по формуле : S = absina , где a и b стороны..sin a - угол между ними..отсюда s = 12*16*sin 150 = 16*6 = 96.
3. Площадь трапеции: S = (a+b)*h и все деленное на 2. остается найти h. через формула (a-b)/2 где a большее основание..найдем проекцию высоты на основание..оно равняется 5..далее по теореме пифагора находим высоту 169= 25+h(квадрат) отсюда h = 12. вернемся к площади ((10+20)*12)/2 = 180