ответ: 3 см
Объяснение (очень подробно):
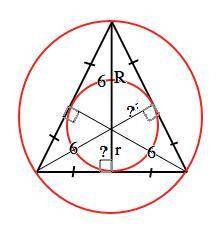
Центром окружности, описанной около треугольника, является точка пересечения его срединных перпендикуляров. В правильном треугольнике центры описанной и вписанной окружностей совпадают. а срединные перпендикуляры – его высоты ( биссектрисы, медианы). Медианы точкой пересечения делятся в отношении 2:1, считая от вершины. Следовательно, радиус R окружности, описанной около правильного треугольника, равен 2/3 его медианы ( высоты), а радиус r вписанной окружности равен 1/3 медианы (высоты).
r=R/2=6:2=3 см.
————————
Задачи на правильные треугольники и окружности, вписанные и описанные около них, встречаются часто. поэтому полезно запомнить это свойство, когда требуется решение без лишних вычислений: r=R/2=6:2=3 см.
Решение: MN = 1/2(BC+AD) = 1/2(5+19) = 12
(BC+MN)/2 = (12+5)/2 = 8,5
h = S(BCMN) / 8,5 = 4
H = 4 * 2 = 8
S(ABCD) = ((5+19)/2)*8 = 96
ответ: 96