Дано:
∠MOH = ∠POH ; Луч НО – биссектриса ∠MHP .
∠MHO =∠PHO = (1/2)*∠MHP - - - - - - - - - - - - - - - - - - - -
1) Док -ать Δ MOH = Δ POH
- - - - - - - - - - - - - - - - - - - -
2) дополнительно : ∠MHO = 42⁰, ∠HMO = 28⁰, ∠НОМ = 110⁰. - - - - - - - - - - - - - - - - - - - -
Найти: ∠OHP - ? ; ∠HPO ; ∠НОР . * * *∠OHP ≡∠PHO * * *
|| ∠OHP - ? ; ∠HPO-? ∠НОР - ? ||
* * * ∠НОМ = 180°-(∠MHO+∠HMO) = 180°-(28⁰ +42⁰) =180°- 70⁰=110⁰
! Второй признак равенства треугольников :
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, такие треугольники равны.
см приложение еще и чертеж

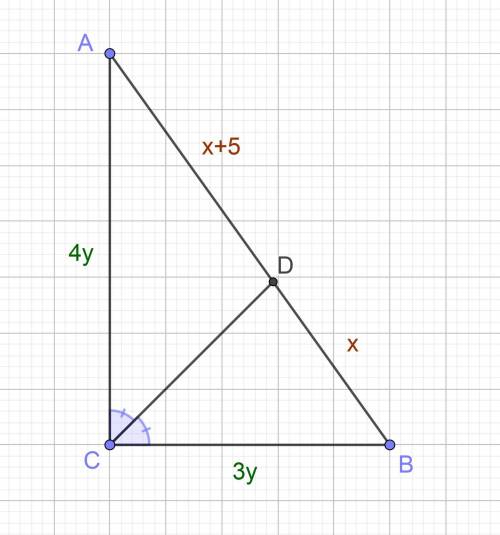
Задача: Биссектриса прямого угла делит гипотенузу прямоугольного треугольника на отрезки, разность которых составляет 5 см. Найдите площадь треугольника, если его катеты относятся как 3:4.
Пусть дан ΔABC, ∠C = 90°, CD — биссектриса. Исходя из условия задачи, обозначим длины отрезков AD за x+5 (см), BD за x (см), AC за 4y (см), BC за 3y (см).
Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника:
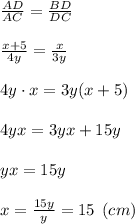
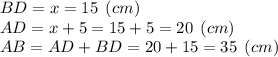
Применим т. Пифагора для определения переменной y:
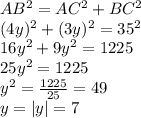
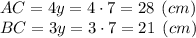
Подставим значения в формулу площади прямоугольного треугольника:
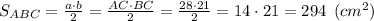
ответ: Площадь треугольника равна 294 см².
с^2=a^2+b^2
подставляем в формулу значения из условий
(2м+1)^2=(3м-3)^2+(2м)^2
4м^2+4м+1=9м^2-18м+9+4м^2
9м^2-22м+8=0
м1=4/9 не подходит так как м натуральное
м2=2
ответ 2