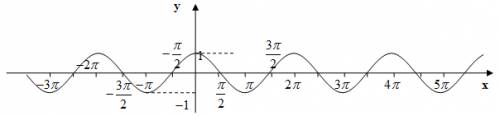
1) Область определения функции - множество всех действительных чисел R
2) Множеством значений функции является промежуток [-1,1]
3) Функция является четной, график симметричен относительно оси Оу.
4) Функция периодическая. Наименьший положительный период равен 2pi
5) График функции пересекает ось Ох (нули функции) в точках pi/2+piK
6) График функции пересекает ось Оy в точке (0; 1).
7) Функция принимает положительные значения на промежутках (-pi/2+2piKб pi/2+2piK)
8) Функция принимает отрицательные значения на промежутках (pi/2+piK, 3pi/2+piK)
9) Функция возрастает на промежутках (-pi+2piK, 2piK)
10) Функция убывает на промежутках (2piK, pi+2piK)
11) Точки минимума: (pi+2piK, -1)
1) √29, √42, √15 большая сторона = √42
(√29)² + (√15)² = 29 + 15 = 44
(√42)² = 42
44 ≠ 42 - нет
2) √2, 3, √7. большая сторона = 3
(√2)² + (√7)² = 2+7 = 9
3² = 9
9 = 9 - ДА
3) √23, √11, √34. большая сторона = √34
(√23)² + (√11)² = 23 + 11 = 34
(√34)² = 34
34 = 34 - ДА
4) √23, 2√2, √31. большая сторона = √31
(√23)² + (2√2)² = 23 + 8 = 31
(√31)² = 31
31 = 31 - ДА
5) √15, √17, √3. большая сторона = √17
(√15)² + (√3)² = 15 + 3 = 18
(√17)² = 17
18 ≠ 17 - нет
6) √30, 2√3, 3√2. большая сторона = √30
(2√3)² + (3√2)² = 12 + 18 = 30
(√30)² = 30
30 = 30 - ДА
7) √15, √30, 4. большая сторона = √30
(√15)² + (4)² = 15 + 16 = 31
(√30)² = 30
31 ≠ 30 - нет