рассмотрим прямоугольный треугольник ABC в которм угол А - прямой, угол В = 30 градусам а угол С = 60.
Приложим к треугольнику АВС равный ему треугольник АВD. Получим треугольник BCD в котором B = D = 60 градусов, следовательно DC = BC. Но по построению АС 1/2 ВС, ч т д
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета равен 30 градусам.
рассмотрим прямоугольный треугольник АВC, у которого катет АС равен половине гипотенузы АС.
Приложим к треугольнику АВС равный ему треугольник ABD. Получит равносторонний треугольник BCD. Углы равностороннего треугольника равны друг другу, поэтому каждый из них = 60 градусам. Но угол DBC = 2 угла ABC, следовательно угол АВС = 30 градусов,ч т д
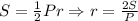
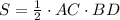
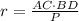
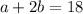- периметр треугольника.
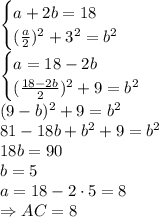
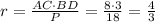
1.5
Объяснение:
Катет что лежит против угла 30 градусов, в два раза больше гипотенузы.
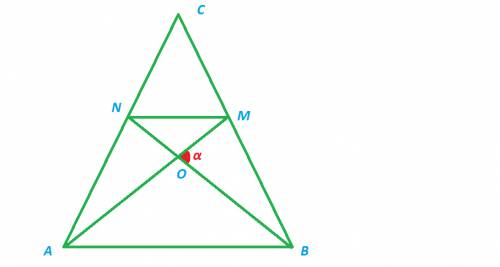
Угол В = 30 ° по скольку вся сторона АВ = 4, а АС = 2. Это же правило подействует и для отрезка МВ, то есть х = 3 : 2 = 1.5