ответ:100 см²
Объяснение: В четырехугольник можно вписать окружность ( или круг) тогда и только тогда. когда суммы противоположных сторон равны.
Трапеция АВСD - четырехугольник. ⇒
ВС+АD=АВ+AD=14+11=25 (см).
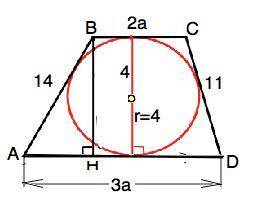
Высота трапеции равна диаметру вписанной окружности. ⇒ ВН=2r=2•4=8
Площадь трапеции равна произведению высоты и полусуммы оснований.
S=h•(a+b)/2=8•25/2=100 см².
----------------------
Как видим, для нахождения площади отношение оснований трапеции является лишним. Но для нахождения длин сторон пригодится.
Примем коэффициент отношения ВС:АD равным а.
Тогда ВС=2а, АD=3а.
ВС+АD=5a=25 (см. выше). ⇒ а=5. ⇒
ВС=2•5=10 см
АD=3•5=15 см.
4; 1), (-3;1), (-2;0), (-4;-1), (-3;-2), (-2;-2), (-1;-1), (-1;-2), (0;-3), (1;-3), (3;-2), (4;0), (4;2), (6;3), (4;3), (5;4), (3;4), (4;5), (4;7), (2;8), (3;6), (2;5), (2;6), (1;8), (1;6), (0;7), (-1;7), (0;6), (0;5), (-1;6), (-2;6), (-3;5), (-2;5), (0;4), (-2;4), (-4;3), (-4;1), (-5;4), (-6;5), (-5,5;3,5), (-7;4), (-7,5;3),
(-6;3), (-8;1), (-7;1), (-6;-2), (-4;-3), (-4; -7), (-3;-8), (-4;-9), (-3;-9),
(-4;-11), (-3;-11), (-2;-9), (-1;-9), (-1;-8), (0,-8), (0;-9), (1;-9), (2;-11), (3;-11), (2;-9), (3; -9), (2;-8), (2;-7), (4;-8), (4;-7), (6;-7), (5; -6), (7;-6), (5;-5), (6;-5), (4;-4), (3;-2).
ГЛАЗ (0;1), (1;1), (1;0), (0,5;0,5).
след. тр.АВР=тр.СВQ
след. ВР=ВQ, след, PBQ - р/б.