1. Ставишь циркуль в вершину угла и проводишь произвольную окружность. Окружность пересекает стороны угла в точках А и В. Ставишь циркуль в точку А,проводишь из нее окружность радиуса АВ. Ставишь циркуль в точку В, проводишь из нее окружность радиуса АВ. Эти две окружности пересекаются в точке С. Соединяешь точку С с вершиной треугольника. Вот тебе биссектрисса.
2. Чертишь произвольно одну из сторон треугольника. Замеряешь циркулем длину второй стороны. Ставишь циркуль на конец первой стороны. Это первая вершина треугольника. Проводишь окружность. Замеряешь циркулем третью сторону, ставишь циркуль на другой конец первой стороны,это вторая вершина треугольника, проводишь окружность. Эти окружности пересекаются в точке А, которая и является третьей вершиной треугольника.
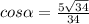
Объяснение:
Дано: Окр.OR-описанная
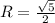
ΔАВС - прямоугольный
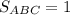
ВК и СМ - медианы
Найти: cosα
1. Окр. OR - описана около ΔАВС ⇒СВ - диаметр (прямой угол опирается на диаметр)

2. Рассмотрим ΔАВС - прямоугольный.
Пусть меньший катет = a, больший - b.
Тогда:
Площадь треугольника:
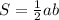
По теореме Пифагора:
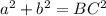
Составим систему:
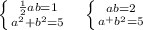
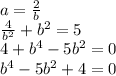
По теореме Виета:

Или
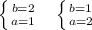
Тогда АС=1; АВ=2.
3. Рассмотрим ΔАВК - прямоугольный.
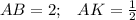 (ВК-медиана)
(ВК-медиана)
По т. Пифагора
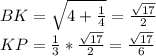 (св-во пересекающихся медиан)
(св-во пересекающихся медиан)
4. Рассмотрим Δ МАС - прямоугольный.
 (СМ-медиана)
(СМ-медиана)
По т. Пифагора
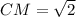
 (св-во пересекающихся медиан)
(св-во пересекающихся медиан)
5. Рассмотрим ΔКРС

Используем теорему косинусов:
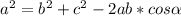
Имеем
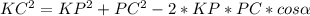

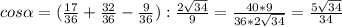

Соединим М1 и М2, N1 и N2. Получим прямоугольные треугольники ММ1М2 и NN1N2. Углы М1 и N1 у них прямые поскольку ММ1 и NN1 перпендикуляры к плоскости. Эти треугольники лежат в параллельных плоскостях поскольку пересекающиеся прямые их сторон перпендикулярны ребру двугранного угла. Следовательно угол ММ2М1= углу NN2N1. Значит эти треугольники подобны как прямоугольные с равным острым углом. Отсюда ММ2/ММ1=NN2/NN1. 5/3=NN2/9. Отсюда NN2=15.