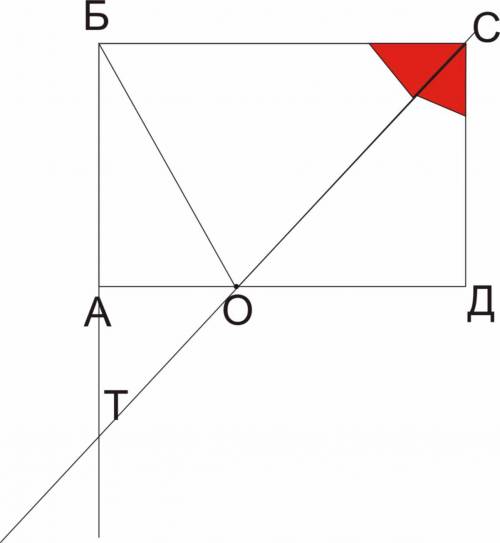
по условию углы БСО = ОСД следовательно они равны по 45 гр. т.к. угол С в прямоугольнике АВСД =90
тр-к ОСД - равнобедренный, т.к. угол ОСД=45 гр., а СДО = 90 гр., следовательно угол СОД=ОСД = 45 гр.
уголы СОД и АОТ - вертикальные - следовательно равны.
ответ: угол АОТ = 45 гр.
или
по условию углы БСО = ОСД следовательно они равны по 45 гр. т.к. угол С в прямоугольнике АВСД =90
углы БСО и СОД равны, как накрест лежащие при параллельных прямых АД и БС
уголы СОД и АОТ - вертикальные - следовательно равны.
ответ: угол АОТ = 45 гр.
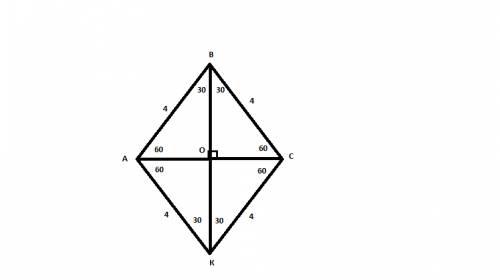
Т к у ромба все стороны раны, и известен периметр, найдем длины сторон: АВ=ВС=СК=АК=16/4=4см.
Рассмотри один из прямоугольных треугольников, образовавшихся при пересечении диагоналей ромба: треугольник АОВ: против угла в 30 градусов (АВО) лежит катет, равный половине гипотенузы, т е АО=4/2=2см. АО=ОС=2см, а ВО=ОК т к диагонали ромба точкой пересечения делятся пополам.
Найдем длину ВО по теореме Пифагора, из треугольника АВО: ВО=ОК=корень из АВ^2-AO^2=корень из 16-4=2корня из 3(см).
Тогда ВК=ВО+ОК=2корня из 3+2корня из 3=4корня из 3(см). АС=АО+ОС=2+2=4см.
Площадь ромба равна половине произведения длин его диагоналей:
S=1/2*АС*ВК=1/2*4*4корня из 3=8корней из3(см^2).
ОТВЕТ: 8корней из3(см^2)
можно к 1 ,2, 3 так как это расшифровывается а в с это стороны , а 4R это радиус поэтому к первым трем