Обозначим хорды АС и АК. Они - касательные, проведенные к меньшей окружности.
Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
⇒. ∠САВ=∠КАВ=60°:2=30°
Проведем СВ и КВ.
∠АСВ=∠АКВ=90° - опираются на диаметр АВ.
∆ АСВ=∆ АКВ - по гипотенузе и острому углу
⇒ АС=АК,
Проведем радиус ОМ в точку касания окружности с АС. Радиус, проведенный в точку касания, перпендикулярен касательной. ⇒
∠АМО=90°
ОМ=r и противолежит углу 30°. ⇒ гипотенуза ОА=2r.
Тогда АВ=3r ⇒
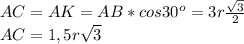
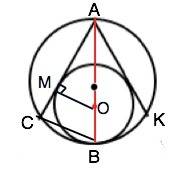
Обозначим хорды АС и АК. Они - касательные, проведенные к меньшей окружности.
Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
⇒. ∠САВ=∠КАВ=60°:2=30°
Проведем СВ и КВ.
∠АСВ=∠АКВ=90° - опираются на диаметр АВ.
∆ АСВ=∆ АКВ - по гипотенузе и острому углу
⇒ АС=АК,
Проведем радиус ОМ в точку касания окружности с АС. Радиус, проведенный в точку касания, перпендикулярен касательной. ⇒
∠АМО=90°
ОМ=r и противолежит углу 30°. ⇒ гипотенуза ОА=2r.
Тогда АВ=3r ⇒

<С = 40*
<В= 100*
ВК- биссектрисса
Найти:<ВКА - ? ; <АВК - ?; < АВК-?
РЕШЕНИЕ.
т.к.АВС - равнобедренный, то угол А = углу
В и равен 40*
ВК- биссектрисса и делит угол АВС пополам ,значит угол АВК = 1/2АВС отсюда 100/2 =50*
угол ВКА = 90*
ответ : <А = 40*; <АКВ= 90*; < АВК=50*