Докажите, что:
а)
середины сторон прямоугольника являются вершинами ромба.
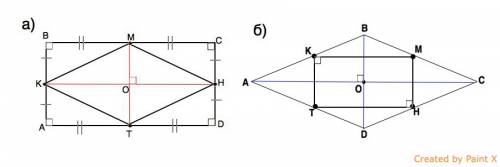
В прямоугольнике все углы прямые, противоположные стороны равны и параллельны, а диагонали равны и точкой пересечения делятся пополам.
Пусть данный прямоугольник АВСD, точки К, М, Н, Т - соответственно середины АВ, ВС, СD, DА.
Соединим последовательно точки К, М, Н и Т
Треугольники КАТ, КВМ, МСН и НDТ прямоугольные, в каждом один катет равен половине меньшей стороны, другой - половине большей стороны. Следовательно, эти треугольники равны, отсюда равны их гипотенузы: КМ=МН=НТ=ТК.
КМНТ - четырехугольник, все стороны которого равны (признак ромба).
Кроме того, диагонали КН║ВС и МТ║АВ.
В прямоугольнике стороны пересекаются под прямым углом, следовательно, параллельные им диагонали КН и МТ тоже пересекаются под прямым углом - признак ромба.
Четырехугольник КМНТ - ромб, и его вершинами являются середины сторон прямоугольника, что и требовалось доказать.
------------------
б)
середины сторон ромба являются вершинами прямоугольника.
Пусть дан ромб АВСD, точки КМНТ - середины его сторон. Соединим их последовательно.
Диагонали ромба АС и ВD пересекаются в точке О под прямым углом и каждая делит ромб на два равных треугольника. АК=КВ, ВМ=МС, СН=НD и DТ=ТА. ⇒
КМ и ТН - средние линии треугольников АВС и СDТ и параллельны диагонали АС ромба.
КМ=ТН
Аналогично ТК и МН - средние линии треугольников АВД и СВD и параллельны диагонали ВD ромба.
КТ=МН.
Стороны четырехугольника ТКМН параллельны и равны - КМНТ - параллелограмм.
Диагонали ромба точкой их пересечения делятся пополам и, пересекаясь, делят четырехугольник ТКМН на 4 равных параллелограмма, углы которых при точке пересечения диагоналей ромба О прямые. ⇒
Углы К, М, Н и Т этих четырех параллелограммов, противоположны углам при О и по свойству углов параллелограмма равны им. Следовательно, четырехугольник ТКМН - параллелограмм, все гулы которого - прямые.
ТКМН - прямоугольник, что и требовалось доказать.
В прямоугольнике все углы прямые, противоположные стороны равны и параллельны, а диагонали равны и точкой пересечения делятся пополам.
Пусть данный прямоугольник АВСD, точки К, М, Н, Т - соответственно середины АВ, ВС, СD, DА.
Соединим последовательно точки К,М,Н и Т
Треугольники КАТ, КВМ, МСН и НDТ прямоугольные, в каждом один катет равен половине меньшей стороны, другой - половине большей стороны. Следовательно, эти треугольники равны, отсюда равны их гипотенузы: КМ=МН=НТ=ТК.
КМНТ - четырехугольник, все стороны которого равны (признак ромба).
Кроме того: диагонали КН║ВС и МТ║АВ.
В прямоугольнике стороны пересекаются под прямым углом, ⇒
параллельные им диагонали ромба КН и МТ тоже пересекаются под прямым углом - признак ромба.
Четырехугольник КМНТ - ромб, и его вершинами являются середины сторон прямоугольника.
3x+3x+x= 49
7x=49
X=7 (cm) - основание.
7× 3 = 21 (см)
ответ: основание - 7см; боковые стороны - 21 см.