В треугольнике ABC, AB = BC. Медианы треугольника пересекаются в точке O, OA = 5, OB = 6. Найдите площадь треугольника ABC.
============================================================
точка О - точка пересечения медиан ( см приложение )По свойству пересечения медиан в ΔАВС ВО:ОЕ = 2 : 1⇒ ОЕ = ВО/2 = 6/2 = 3 По свойству равнобедренного треугольника ВЕ⊥АС, ВЕ - медиана, высота, биссектрисаВ ΔАОЕ: по теореме ПифагораАЕ² = АО² - ОЕ² = 5² - 3² = 25 - 9 = 16АЕ = 4АС = 2•АE = 2•4 = 8Значит, S abc = BE•AC/2 = 9•8/2 = 36ОТВЕТ: S abc = 36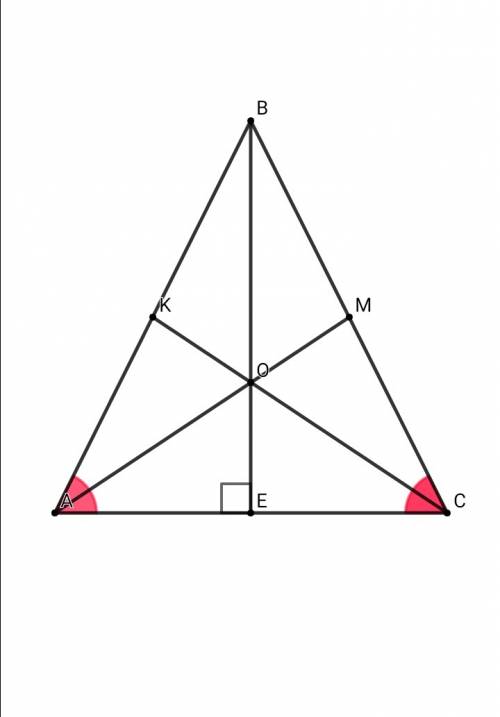
Объяснение:
Багато видів організмів набули здатності переживати несприятливі умови (високу або дуже низьку температуру, зниження вологості, відсутність їжі тощо) у стані глибокого спокою. Він характеризується зниженням фізіологічних процесів, уповільненням газообміну, припиненням живлення і нерухомістю тварин. Температура, за якої настає такий стан, різна для різних видів. У деяких комах, риб і земноводних глибокий спокій настає вже в разі зниження температури до +15 °С, у інших -- при +10 °С, а у деяких -- лише за температури, близької до 0 °С.
В треугольнике углы А=В, ⇒
∆ АСВ – равнобедренный.
Угол ВСА=180°-2•75°=30°
Проведем высоту АН.
Примем АН=х
Тогда гипотенуза АС=2х, т.к. АН противолежит углу 30°
S (ABC)=BC•AH/2
ВС=АС=2х
S=х•2х.2=36⇒
х²=36⇒
х=6
ВС=2х=12 см