Объяснение:
Дано:
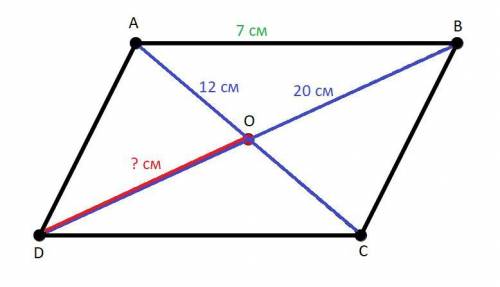
ABCD - параллелограмм.
AC и BD - диагонали параллелограмма.
AC ∩ BD = O.
AC = 12 (см); BD = 20 (см); AB = 7 (см).
Найти:
DO - ? (см).
Тут всё довольно просто. Так как ABCD - параллелограмм, вспомним свойство такой геометрической фигуры: диагонали параллелограмма точкой пересечения делятся пополам. Т.е. диагонали AC и BD делятся точкой пересечения O пополам. Соответственно DO будет равняться половине всей диагонали BD. (и из этого следует, что DO = OB)
DO = BD/2 = 20 : 2 = 10 (см)
в прямоугольной трапеции опустим перпендикуляр из точки С на сторону АД...получится..что левая часть нижнего основания равна 2.25 а правая 4 см..
по теореме пифагора в левой части из прямоугольного треугольника найдем опущенный перпеникуляр(высота)..он равен = 3 см..значит и параллельная ему сторона тоже равна 3 см..отсюда можно найти периметр = 16.5
найдем первую диагональ: так же по теореме пифагора где катеты равны 2,25 см и 3 см..1-я диагональ равна = 15/4 = 3.75 см.
2-я диагональ..так же из теоремы пифагора где катеты 3 и 6.25 2-я диагональ равна = (корень из 769 деленное) на 4.