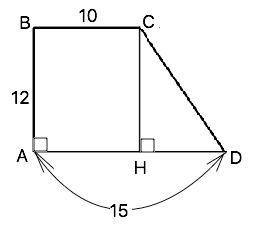
В трапеции ABCD основания AD и BC равны 15см и 10см соответственно, угол А = 90°, АВ = 12 см. Найдите периметр трапеции.
ответ: 50 см
Объяснение:
Периметр многоугольника - сумма длин всех его сторон. Известны три стороны трапеции, следует найти боковую сторону СD.
Опустим высоту СН. Треугольник СНD - прямоугольный с катетами СН и НD и гипотенузой СD.
АВСН - прямоугольник ( АН||ВС, СН||АВ, АВ и СН перпендикулярны основаниям).
СН=АВ=12.
АН=ВС=10
НD=АD-АН=15-10=5 (см)
По т.Пифагора СD=√(CH²+HD²)=13 см
P=AB+BC+CD+AD=12+10+13+15=50 см
Длина Н высоты равна:
H = 2S/a, где а - меньшая сторона.
Площадь S находим по формуле Герона.
S = √(p(p-a)(p-b)(p-c)).
Полупериметр р = (7+16+13)2 = 36/2 = 18.
S = √(18*11*2*5) = √ 1980 ≈ 44,497191.
ответ: Н = 2* 44,497191 / 7 = 12,71348.