ответ: Р=162 см
Объяснение:
Пусть дана прямоугольная трапеция ABCD. у которой ВС и AD - основания, угол А =углу В=90 градусов. О- центр вписанной в трапецию окружности, точка М - точка касания окружности стороны AD и точка К - точка касания окружности стороны ВС. АМ=20 см, MD=25 см, тогда ОМ=ОК=r=20см и АВ=40 см. DM=DK=25 см как отрезки касательных,проведенных из одной точки. Угол С+ угол D трапеции=180 градусов, как внутренние накрест лежащие углы, DO и CO - биссектрисы соответствующих углов, то угол CDO+DCO=90градусов, следовательно угол COD=90 градусов, т.е. треугольник COD - прямоугольный, у которого ОК - высота, проведенная к гипотенузе, OK^2=DK*CK, CK=400/25=16 см. Значит периметр трапеции равен 20+25+25+16+16+20+40=162 см
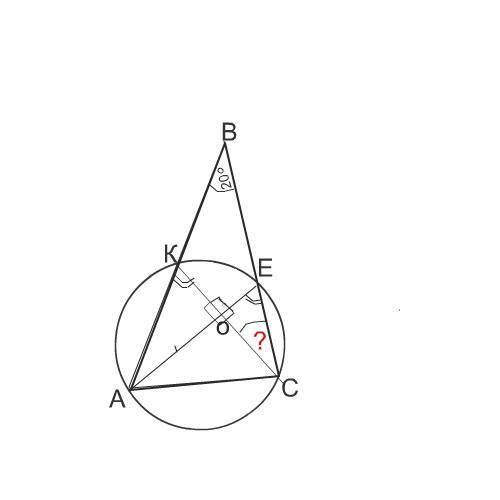
Сделаем рисунок к задаче.
Рассмотрим треугольники АКС и АЕС. Углы при К и Е в них равны, так как являются вписанными углами опирающимися на одну и ту же дугу, стягиваемую хордой АС.
Следовательно углы ВКС и ВЕА тоже равны как смежные с ними.
Угол КОЕ прямой по условию задачи.
Сумма углов четырехугольника равна 360°
Сумма равных углов ВКС и ВЕА равна
360-90-20=250°
Углы эти равны по 250:2=125°
Смежные с ними углы АЕС и АКС равны по 180-125= 55°
Сумма углов треугольника равна 180°
Так как угол ЕОС прямой, угол КСВ равен 180-90-55=35°
Пример:Аксиома параллельных прямых. Через любую точку, лежащую вне прямой, можно провести другую прямую, параллельную данной, и притом только одну.