ответ:В задачах этого параграфа двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, для краткости будем называть так: двугранный угол CABD.
Дано: ABCD - тетраэдр;
Определим линейную меру двугранного угла DACB.
ADC ⊥ пл. АВС, тогда двугранный угол DACB и соответствующий ему линейный угол DCB равны 90о.
Определим линейную меру двугранного угла DABC.
Проведем отрезок СМ ⊥ АВ, соединим точки М и D.
то по теореме о 3-х перпендикулярах,
По определению, ∠DMC - линейный угол двугранного угла DABC.
По теореме Пифагора:
Тогда
Отсюда
Определим линейную меру двугранного угла BDCA.
то ∠АВС - линейный угол двугранного угла
Объяснение:
1. 12 * 7 = 84 см"
2. 24 см
3.49√2 см
4. -----------
5.24√2 см²
Объяснение:
1. Тут и так понятно)
2. Высота поделила основу пополам,тем самым поделив треугольник на 2 маленьких.По теореме Пифагора квадрат гипотенузы = сумме квадратов катетов. Найдём катет( половину основы треугольника).
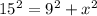
225 = 81 +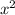 
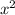= 225 - 81 = 144
х =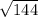 
= 12 см
Теперь узнаем длинну основы: 12 +12 = 24 см
3.Площадь ромба через его сторону и угол
S = a²·sin(β) = (7√2)²·sin(135°) = 49*2 * 1/√2 = 49√2 см
4. Не знаю, прости((((
5.Дано: трапеція КМРТ, МР=7 см, КТ=9 см, ∠Т=45°.
Проведемо висоту РН. Розглянемо ΔРТН - прямокутний.
∠Т=45°, тоді ∠ТРН=90-45=45°, тобто ΔРТН - рівнобедрений.
Нехай РН=ТН=х см, тоді за теоремою Піфагора
х²+х²=6²; 2х²=36; х²=18; х=√18=3√2; РН=3√2 см.
S=(МР+КТ):2*3√2=(7+9)/2*3√2=24√2 см²
