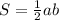
1. Если построить ВСЕ ТРИ треугольника, образованные высотой пирамиды, апофемой и её проекцией на основание, то это будут прямоугольные треугольники с равными острыми углами, поскольку грани равнонаклонены к основанию. Поэтому равны все апофемы, и - главное - равны их проекции на основание.
То есть проекция вершины пирамиды - это точка, равноудаленная от сторон основания, то есть центр вписанной в основание окружности.
2. В плоскости этого треугольника (можно взять любой из трех, они одинаковые) лежит и отрезок от точки на высоте до стороны основания, заданный в условии, - этот отрезок соединяет эту точку с вершиной апофемы, и образуется равнобедренный треугольник, внешний угол при вершине у которого равен π/2 - β (я считаю, что угол β - это угол между этим отрезком и плоскостью основания, в условии тут неточность - если задан угол с боковой гранью, то β' <=> π/4 - β/2 ). Поэтому острые углы этого равнобедренного треугольника равны π/4 - β/2, причем один из них - это угол между апофемой и высотой пирамиды.
Поэтому радиус вписанной в основание окружности равен
r = h*tg(π/4 - β/2);
3. С другой стороны, катеты прямоугольного треугольника в основании равны
a = r*(1 + tg(α/2)); b = r*(1 + ctg(α/2));
откуда площадь основания
S = r^2*(1 + tg(α/2))*(1 + ctg(α/2))/2 = r^2*(1 + 1/sin(α)) = h^2*(1 + 1/sin(α))*(tg(π/4 - β/2))^2 = h^2*(1 + 1/sin(α))*(1 - sin(β))/(1 + sin(β));
Объем пирамиды равен
V = S*h/3 = (h^3/3)*(1 + 1/sin(α))*(1 - sin(β))/(1 + sin(β));
1. Я продолжаю катеты за вершины острых углов - катет a на величину второго катета b, и наоборот. Если через полученные точки, отстоящие от вершины прямого угла треугольника на (a + b), провести линии параллельно катетам до пересечения, то получится квадрат со стороной (a + b).
2. Вершины квадрата, построенного на гипотенузе, лежат на сторонах построенного квадрата (подобное построение используется в одном из доказательств теоремы Пифагора).
3. Если повернуть построенный квадрат (со стороной (a + b) ) на 90° вокруг его центра, то он перейдет "сам в себя". При этом вершины вписанного в него квадрата, построенного на гипотенузе исходного треугольника, тоже перейдут в себя. Поэтому центры этих квадратов совпадают.
4. Таким образом, отрезок p, соединяющий вершину прямого угла с центром квадрата, построенного на гипотенузе, равен половине диагонали квадрата со стороной (a + b) и образует с катетами углы в 45°. Его величина равна p = (a + b)√2/2;
5. Отрезок q, соединяющий центры квадратов, построенных на катетах, очевидно, проходит через вершину прямого угла, равен q = (a + b)√2/2 и тоже образует с катетами углы 45°. Поэтому отрезки p и q взаимно перпендикулярны, и можно считать p высотой в заданном в задаче треугольнике (при этом q - основание).
Окончательно S = p*q/2 = (a + b)^2/4 = (6 + 8)^2/4 = 49